
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
F f f f
|
|
|
|
що зумовлено водневими зв’язками. Кут між зв’язками ÐHFH дорівнює 134о. Як показує визначення густини пари, навіть при температурі, близь-кій до точки кипіння, середній склад фтороводню приблизно відповідає формулі (HF)4. Асоціація молекул спричинює аномально високі темпера-тури плавлення й кипіння фтороводню порівняно з водневими сполуками інших елементів головної підгрупи сьомої групи. Енергія водневого зв’язку становить 8 – 40 кДж/моль і за міцністю дещо перевищує енергію вандерваальсової взаємодії, проте набагато менша за енергію ковалентного зв’язку.
Енергія водневого зв’язку зменшується зі збільшенням температури. Водневий зв’язок відіграє важливу роль при асоціації молекул, кристалі-зації, розчиненні, утворенні кристалогідратів, електролітичні дисоціації, у хімії органічних сполук, особливо вуглеводів, білків, нуклеїнових кислот.
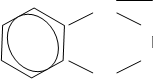
Водневий зв’язок може виникати не лише між атомами різних молекул, а й між атомами однієї молекули, що особливо характерно для органічних речовин. Одним із типових прикладів може служити внутріш-ньо-молекулярний водневий зв’язок у молекулі орто-нітрофенолу:
 N----- O
N----- O
O
H
O
Тема 5. ОСНОВИ ХІМІЧНОЇ ТЕРМОДИНАМІКИ
У попередніх темах курсу було висвітлено закономірності будови атомів і молекул, утворення молекул із атомів і йонів, побіжно схаракте-ризовано міжмолекулярні взаємодії. Однак одержані знання не дозволя-ють знайти відповіді на ряд запитань, які ймовірно найбільш важливі при проектуванні нових технологічних процесів, при розробці технологічного устаткування, створенні систем автоматизації та технічного контролю.
Чи здійсненні в принципі потрібні для даного технологічного проце-су хімічні перетворення? Якщо ці перетворення можливі, то за яких умов? Якою є глибина хімічних змін, що визначаються. Як оцінити хіміч-ну активність чи стабільність використовуваних чи одержуваних речовин та продуктів? Чи існують за однакових або близьких вихідних умов аль-тернативні шляхи хімічних перетворень, і якщо так, то яка ймовірність їх-нього перебігу? Чи можливо так підвищити вибірковість процесу, щоб економічні витрати на його проведення зробити найменшими, з найбіль-шим виходом цільового продукту та найменшим побічних.
Матеріал теми, яку викладено далі дозволяє відповісти на деякі з подібних запитань. Відповіді на інші запитання вимагають залучення на-ступних тем курсу (чи навіть курсів), для яких дана тема є головним підґрунтям.
Поняття про процесовий ансамбль частинок.
Будь-який процес можна подати послідовністю перетворень (розри-ву, сполучення, рекомбінації тощо) зв’язків під впливом якихось сил. У реальних процесах із участю великих кількостей речовин, у будь-якій частині об’єму реактора щосекунди видозмінюються міріади зв’язків між такого ж порядку кількістю частинок. У таких умовах простежувати поведінку кожної частинки, а тим більше керувати нею є справою безна-дійною.
На щастя поведінка частинок-учасниць процесу не є довільною, а є обмеженою взаємодією між ними. Тому, як і у великому оркестрі, де кожна група музичних інструментів, підпорядковуючись єдиному зв’язу-ючому їх керуванню, виконує частину музичної фрази, так і кожна група частинок, відмінних за природою, складом, енергією, стереометрією, ви-конує свою частину окремої хімічної дії. Така множина частинок, об’єд-наних єдиною самоузгодженою чи керованою дією – процесом, і назива-ється процесовим ансамблем.
У підсумку процесу всередині ансамблю перерозподіляється енергія, змінюється імпульс частинок, змінюються їхні магнітні та електричні ха-рактеристики. Однак із курсу фізики відомо, що середньостатистичною мірою енергії частинок ансамблю є температура T [K] ансамблю; його об’єм V [м3] відображує середньостатистичне співвідношення кінетичної та потенціальної енергії; тиск р [Па] відповідає середнім значенням ім-пульсу; напруженості електричного Е [B/м] та магнітного Н [A/м] полів визначають середньостатистичні електричні й магнітні характеристики частинок, концентрація Сі [мас. %; моль/л; моль/кг; мольн.%] відображує кількісне співвідношення частинок різного типу. Безпосередньо вимірювані величини, такі як Т, р, V, Сі , Н, Е, тощо, які середньостатис-тично відображують якусь із якостей частинок, що складають ансамбль, називаються параметрами. Набір числових значень параметрів визначає стан ансамблю. Оскільки параметри будь-якого ансамблю пов’язані рівнянням стану, то частина параметрів виявляється залежною, тобто визначається з рівняння стану, за умови, що інші параметри – незалежні – задано чи визначено дослідним шляхом. Очевидно, що контролюючи та керуючи змінами параметрів, ми встановлюємо чи спрямовано змінюємо стан ансамблю й, таким чином, контролюємо чи скеровуємо середньо-статистичний перебіг процесу. При цьому, щоб задати стан ансамблю нам необхідно задати (чи знати) рівняння стану та числові значення незалежних параметрів. Щоб довільно змінювати стан необхідно змінити хоча б один із параметрів. Для спрямованої зміни стану необхідно змінити значення незалежних параметрів.
Приклад 1. Нехай рівняння стану деякого ансамблю має вигляд: 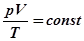 . Які з параметрів p, V, T необхідні, щоб задати стан довільно чи спрямовано його змінити?
. Які з параметрів p, V, T необхідні, щоб задати стан довільно чи спрямовано його змінити?
Відповідь. З трьох параметрів два є незалежними, а третій, що визнача-ється з рівняння стану, залежний. Отже, щоб задати стан ансамблю необхідно задати числові значення двом із даних параметрів: p та V, p та T чи V та T. Третій при цьому визначається як 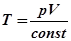 ;
; 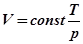 ;
; 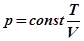 . Ті ж пари параметрів слід змінювати й при спрямованій зміні стану. При довільній зміні можна змінювати будь-який із параметрів p, V чи T.
. Ті ж пари параметрів слід змінювати й при спрямованій зміні стану. При довільній зміні можна змінювати будь-який із параметрів p, V чи T.
Уявлення про фізико-хімічну систему.
Фізико-хімічною системою називається деяка область простору М, відокремлена справжньою чи умовною оболонкою W від навколишнього простору D та вміщуючи у собі повністю чи частково деякий процесовий ансамбль. Очевидно, що при такому визначенні набір параметрів, стан і рівняння стану ансамблю та вміщуючої його системи співпадають, а ха-рактер взаємодії в ансамблі (фізичний фізико-хімічний, біологічний соці-альний, тощо) задає характер системи. Що ж стосується типу системи, то він визначається властивостями оболонки, через яку система взаємодіє з навколишнім середовищем.
Дійсно, у найбільш загальному випадку, система, де перебігає деякий процес, виконує роботу А, використовуючи для цього як власну енергію Еin, так і енергію навколишнього середовища Еex. Припускаючи, що система М та середовище D обмінюються роботою та енергією через оболонку W, одержуємо, що тип системи визначається “прозорістю” цієї оболонки відносно потоків енергії та роботи (див. мал.5.1).



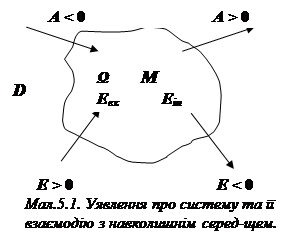 При цьому додатнім буде вважати-ся надходження енергії до системи та виконання останньою роботи з перетво-рення навколишнього середовища.
При цьому додатнім буде вважати-ся надходження енергії до системи та виконання останньою роботи з перетво-рення навколишнього середовища.
Тепер класифікація типів системи, подана на мал.2 включає чотири типи систем: ізольовану (W не “прозора” ані для роботи, ані для енергії, тобто систе-ма нічим не обмінюється із навколишнім середовищем), замкнену (оболонка W
“прозора” для енергії, але не для роботи) адіабатну (W “прозора” для роботи, але не пропускає енергії) та, нарешті, відкриту (здатна обмінюватися із навколишнім середовищем як роботою, так і енергією).
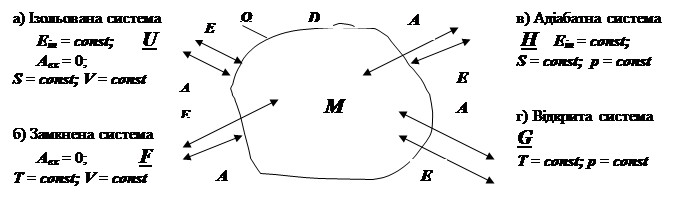 |
Мал.5.2. Класифікація типів систем.
Щоб виділити характерні особливості поведінки означених типів систем, які відображують (із відомою ідеалізацією) характеристики бага-тьох реальних об’єктів дослідження розглянемо перш за все специфіку роботи та природу енергії у фізико-хімічних системах.
Робота фізико-хімічної системи.
Відомо, що робота є добутком деякої узагальненої сили F на спряже-ний із нею параметр l, який характеризує рух системи під дією цієї сили: А = F × l. Диференціюючи це рівняння, одержимо dA = Fdl + ldF. Якщо подати диференційне рівняння у скінчених різницях, воно виглядатиме:
DA = F(lk – l0) + l(Fk – F0) (1a)
Позначивши DA = Аt; F(lk – l0) = Aex; l(Fk – F0) = Ain, одержимо:
At = Aex + Ain, (1б)
де At – повна робота здійснювана системою; Aex – її зовнішня складова, тобто та робота, якою система через оболонку W впливає на навколишнє середовище; Ain – внутрішня робота, тобто та робота, яку система вико-ристовує для власного перетворення і яка ніяк не впливає на навколишні системи.
Приклад 2. Нехай роботу задано добутком тиску на об’єм системи: 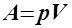 . Визначити значення At, Aex, та Ain.
. Визначити значення At, Aex, та Ain.
Відповідь. Диференціюючи 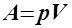 , одержуємо dA = рdV + Vdp. Заміню-ючи диференціальний вигляд на вигляд у скінчених різниці маємо: DA = Аt; р(Vk –V0) = Aex; V(pk – p0) = Ain.
, одержуємо dA = рdV + Vdp. Заміню-ючи диференціальний вигляд на вигляд у скінчених різниці маємо: DA = Аt; р(Vk –V0) = Aex; V(pk – p0) = Ain.
Очевидно, що в системі на малюнку 2 стрілки передбачають обмін тільки зовнішньою роботою, відносно якої слід розглядати “прозорість” оболонки. Що ж стосується внутрішньої роботи то енергія, використана для її здійснення, залишилась всередині системи й лише якось перерозпо-ділялась після виконаної дії перетворення внутрішньо системних зв’язків. Приклади виразів для внутрішньої роботи подано втаблиці 1.
Таблиця 5.1.
ЗНАЧЕННЯ ДЕЯКИХ ВИДІВ ЗОВНІШНЬОЇ РОБОТИ
| Тип роботи | Математичний вираз | Позначення |
| Робота розширення | Aex = р(Vk –V0) | р = const – тиск у системі; Vk та V0 – відповідно кінцевий та початковий об’єми системи |
| Робота сил поверхне-вого натягу | Aex = – s(Sk –S0) | s = const – поверхневий натяг; Sk та S0 – відповідно кінцева та початкова величина площі |
| Робота однорідної де-формації твердого тіла | 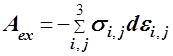
| sI,j = const – нормальні та зсу-вові компоненти напруги; ei,j – компоненти деформації. |
| Робота поляризації діелектрика | Aex = – Е(Рk –Р0) | Е = const – електричне поле у діелектрику з індукцією D; Рk та Р0 – відповідно кінцева та початкова поляризації. |
| Робота намагнічування магнетика | Aex = – H(Mk –M0) | H = const – магнітне поле у магнетику з індукцією B; Mk та M0 – відповідно кінцевий та початковий вектори намагніч. |
| Робота хімічної реакції | 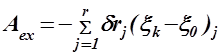
| δrj = const – хімічна спорідне-ність реакції j; xk та x0 – ступе-ні повноти реакції j. |
З поданих виразів випливає, що характер впливу на навколишнє середовище та спосіб передачі роботи через оболонку різний та залежить від виду роботи. Логічно припустити, що кожному видові роботи, відпо-відають різні види енергії.
Енергія фізико-хімічної системи.
У сучасній хімії виокремлюють п’ять типів енергії.
Внутрішня енергія (U) – сума кінетичних і потенціальних енергій усіх частинок ансамблю, що заповнюють систему, яка не виконує зовніш-ньої роботи, тобто Аех = 0.
Ентальпія (Н) – сума кінетичних і потенціальних енергій усіх частинок ансамблю, що заповнюють систему, яка виконує зовнішню ро-боту, тобто Аех ¹ 0.
Вільна енергія Гельмгольца (F) являє собою ту частину внутріш-ньої енергії, яку у даному стані можна перетворити у роботу.
Вільна енергія Гібса (G) – та частина ентальпії Н, яку можна пере-творити у роботу у даному стані.
Зв’язана енергія (TS) являє собою ту частину внутрішньої енергії чи ентальпії, яку у даному стані не можна перетворити у роботу.
Віднесемо повністю чи частково роботоспроможні енергії (U, H, FG) до І класу, а роботонеспроможну (TS) до ІІ класу. Оскільки усі енергії пов’язані з роботою, то їхня розмірність, як і розмірність різних видів роботи At, Aex, та Ain співпадають [Дж/моль; Дж/кг] або [Дж, кДж, МДж].
Взаємозв’язок видів енергій та видів робіт, що випливає з вище на-ведених визначень подано на малюнку 5.3. Зі схеми випливає ряд співвідношень між видами енергії та роботи фізико-хімічної системи:
Н = U + Aex; F = U – TS; G = Н – TS; G = F + Aex;
U = F + TS = Ain + TS; Н = G + TS = At + TS = Aex + Ain + TS.
 Aex
Aex
G (At )
 H F Ain
H F Ain

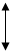 U
U
TS
 |
Мал.5.3. Схема взаємозв’язку енергій і робіт фізико-хімічної системи.
Вияснимо тепер, як змінюється енергії І та ІІ класів під час перебігу процесів (перетворень).
Самодовільність (спонтанність) процесу.
Самодовільним (спонтанним) називається процес, який здійснює ся за рахунок власної енергії системи. Несамодовільним (неспонтан-ним) є той процес, який можна здійснити тільки підводячи до системи енергію ззовні. Нарешті, рівноважним є процес, у якому рівно ймовірні самодовільні як прямий так і зворотній напрямки.
Приклади самодовільних за нормальних умов процесів:
BaCl2 + CuSO4 ® BaSO4 + CuCl2;
Zn + 2HCl ® ZnCl2 + H2;
HCl + NaOH ® NaCl + H2O;
Be(OH)2 + 2NaOH ® Na2[Be(OH)4];
Приклади несамодовільних без підведення додаткової енергії за нормальних умов процесів:
СН3СН2ОН + СО2 ® СН3(СНОН)СООН;
СаСО3 ® СаО + СО2;
2СоО + О2 ® 2Со2О3;
3О2 ® 2О3.
Приклади рівноважних за нормальних умов процесів, у яких від-окремлення продуктів реакції та вихідних речовин малоймовірне:
NaNO3 + KCl Û KNO3 + NaCl;
2NO2 Û N2O4;
NaHCO3 + H2O Û NaOH + H2CO3.
Логічно припустити, що в усіх трьох типах процесів зміни енергії будуть відмінними. Для відповіді на це запитання розглянемо механічну систему *, що складається з параболічної вигнутої догори поверхні, на яку поміщено кульку (мал.5.4) у позиціях “а” та “б”.__________________
* Висновки одержані на підставі механічної системи справедливі й для будь-якої іншої (фізичної, фізико-хімічної, біологічної, соціальної, тощо) системи.
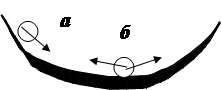 З аналізу цієї системи випливає:
З аналізу цієї системи випливає:
1. Найбільш стійким станом системи є рівноважний стан (позиція “б”). Усі не-рівноважні стани є нестійкими.
|
|

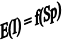










 3. Чим більш нерівноважна система, тим більша її енергія та роботоспроможність. Отже в самодовільних процесах енергія І класу зменшується, а у стані рівноваги стає мінімальною.
3. Чим більш нерівноважна система, тим більша її енергія та роботоспроможність. Отже в самодовільних процесах енергія І класу зменшується, а у стані рівноваги стає мінімальною.
|

 4. Чим більш нерівноважна система, тим менше у ній нероботоспроможних зв’яз-ків, тобто тим нижче рівень енергії ІІ класу. Отже у самодовільному процесі енергія ІІ класу зростає та досягає макси-муму у стані рівноваги.
4. Чим більш нерівноважна система, тим менше у ній нероботоспроможних зв’яз-ків, тобто тим нижче рівень енергії ІІ класу. Отже у самодовільному процесі енергія ІІ класу зростає та досягає макси-муму у стані рівноваги.
5. У стані рівноваги роботоспроможні види енергії мінімальні, а зв’язана максимальна. Отже, у рівноважному стані роботоспроможність системи мінімальна та може забезпечити лише рекомбінаційні переходи на кшталт іонної рівноваги, таутомерних або дзеркальних перетворень. У самодові-льних процесах система перетворює навколишнє середовище, а у несамо-довільних середовище впливає на систему.
На підставі зроблених висновків подано графіки зміни енергій І (ЕІ, ЕІ = U, H, FG) та ІІ (ЕІІ, ЕІІ = TS) класів у залежності від відхилення системи від стану рівноваги (мал.5.5). За початок координат прийнято рівноважний стан “р”. На параболах, що відповідають (умовно) функціям ЕІ =f(Sp), ЕІ =U, H, FG та ЕІI =f(Sp), ЕІІ = TS, де Sp має зміст відхи-лення від стану рівноваги, нанесено процеси: 1 ® 2 та 1¢ ® 2¢ – самодовільні 3 ® 4 та 3¢ ® 4¢ – несамодовільні 5 ® 6 та 5¢ ® 6¢ – рівноважні. Тоді:
а) DЕІ = ЕІ2 – ЕІ1 < 0; DЕІІ = ЕІІ2 – ЕІІ1 > 0 – процеси самодовільні;
б) DЕІ = ЕІ6 – ЕІ5 = 0; DЕІІ = ЕІІ6 – ЕІІ5 = 0 – процеси рівноважні;
в) DЕІ = ЕІ4 – ЕІ 3 > 0; DЕІІ = ЕІІ4 – ЕІІ3 < 0 – процеси несамодовільні;
На підставі одержаних висновків складемо таблицю критеріїв самодовільності процесів.
Таблиця 5.2.
Критерії самодовільності процесів різних класів енергій.
| Критерій | Процеси | ||
| самодовільний | рівноважний | несамодовільний | |
| DU DH DF DG | < 0 < 0 < 0 < 0 | = 0 = 0 = 0 = 0 | > 0 > 0 > 0 > 0 |
| TDS | > 0 | = 0 | < 0 |
Методи розрахунку значень змін енергетичних функцій
у фізико-хімічних процесах.
Значення, а головне, знак значень DU, DH, DF, DG та TDS можливо визначити на підставі закону Г.І. Геса: “Якщо з даних вихідних речовин можна одержати задані кінцеві продукти різними шляхами, то сумарна теплота процесу на одному якому-небудь шляху дорівнює сумарній теп-лоті процесу на будь-якому іншому шляху, тобто не залежить від шляху переходу від вихідних речовин до продуктів реакції”.
Наприклад водний розчин хлориду амонію можна одержати двома шляхами:
І) NH3 + H2O Û NH3,aq, Q1; HCl + H2O Û HClaq, Q2;
NH3,aq + HClaq, Û NH4Claq, Q3.
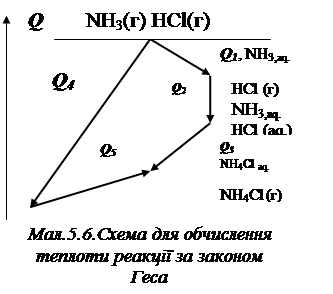
ІІ) NH3(г) + HCl(г) Û NH4Cl(г), Q4; NH4Cl(г) + H2O Û NH4Claq, Q5.
 У наведених реакціях “aq” означає водний розчин даної речовини, Qi – відповідне значення теплового ефекту.
У наведених реакціях “aq” означає водний розчин даної речовини, Qi – відповідне значення теплового ефекту.





 Для наведених процесів властива схема, подана на малюнку 5.6. Зі схеми випли-ває, що, оскільки початковий та кінцевий стани однакові, то справедливо:
Для наведених процесів властива схема, подана на малюнку 5.6. Зі схеми випли-ває, що, оскільки початковий та кінцевий стани однакові, то справедливо:

 Q1 + Q2 + Q3 = Q4 + Q5.
Q1 + Q2 + Q3 = Q4 + Q5.

 Перед тим, як зробити висновок із зако-ну Геса введемо наступні визначення:
Перед тим, як зробити висновок із зако-ну Геса введемо наступні визначення:

 1. Енергія, яка виділяється при утворенні 1 моля даної речовини з вихідних прос-тих речовин, називається енергією утво-рення даної речовини. Позначається
1. Енергія, яка виділяється при утворенні 1 моля даної речовини з вихідних прос-тих речовин, називається енергією утво-рення даної речовини. Позначається
така енергія DЕ0f [кДж/моль]. Якщо ж визначають енергію утворення іншої кількості речовини, то DЕf = DЕ0f× n [кДж]. Для багатьох речовин значення DЕ0f виміряно за стандартних умов (Т = 298 К, р = 1,013 × 105 Па) та табульовано у вигляді DU0f, DH0f, DF0f та DG0f. А щодо зв’язаної енергії TDS то табулюється лише її енергетична складова, яку називають ентропією утворення: S0f [Дж/(моль × K)], зміст якої буде визначено піз-ніше. Значення DU0f, DH0f, DF0f, DG0f та S0f залежать від температури. То-му, якщо температура відрізняється від стандартної, то пишуть DU0f,500, DH0f,1200, DG0f,163, тощо. Енергії утворення DU0f, DH0f, DF0f та DG0f простих речовин дорівнюють нулю. Ентропія утворення будь-якої речовини, у тому числі й простої, більша за нуль (S0f > 0).
2. Енергія, яку потрібно затратити, щоб розкласти дану речовину до прос-тих речовин, називається енергією розкладу. Позначається ця енергія DЕ0d (DU0d, DH0d, DF0d, DG0d). Аналогічно існує і S0d. До енергій та ентро-пії розкладу стосується все те, що було сказано вище стосовно до енергій та ентропії утворення.
Тепер можна сформулювати наслідки з закону Геса та визначити розрахункові методи.
Наслідок 1. (закон Лавуазьє-Лапласа) Енергії утворення та розкладу од-нієї речовини однакові за величиною, та протилежні за знаком:
DЕ0f = – DЕ0d.
Наслідок 2. Енергетичний ефект фізико-хімічного процесу дорівнює різ-ниці сум відповідних енергій утворення продуктів та енергій утво-рення вихідних речовин.
Нехай має місце реакція: a A + b B ® k K + m M, де A, B, K та M – по-значення хімічних речовин, а a, b, k та m – стехіометричні коефіцієнти при них. Нехай також для кожної речовини відомі енергії утворення за стандартних умов: DЕ0f ,A, DE0f ,B, DE0f ,K та DE0f ,M. Тоді енергетичний ефект реакції DЕ0r дорівнюватиме:
DЕ0r = (kDE0f,K+ mDE0f,M) – (aDЕ0f,A + bDE0f,B).
Деякі особливості інтерпретації підсумків термохімічних розрахунків.
І. На підставі термохімічних розрахунків визначимо енергетичні (ентальпійні) ефекти реакцій синтезу соляної кислоти та розкладу води за стандартних умов: а) H2(г) + Cl2(г) ® 2HCl(г); DH0r1 =?;
б) 2H2О(р) ® 2Н2(г) + О2(г); DH0r2 =?.
Перепишемо рівняння реакцій у вигляді:
½H2(г) + ½Cl2(г) ® HCl(г); DH0rА =?; H2О(р) ® Н2(г) + ½О2(г); DH0rВ =?.
Рівняння реакцій приведені до одного моля вихідної речовини чи кінце-вого продукту називаються термохімічними. Випишемо з таблиці значен-ня: DH0f (H2O) = – 285,85 кДж/моль; DH0f (HCl) = – 92,3 кДж/моль.
Ентальпії утворення H2, O2, Cl2(простих речовин) дорівнюють нулю, тоді:
DH0rА = DH0f (HCl) – (½ DH0f (H2) + ½ DH0f (Cl2)) = – 92,3 – (½ · 0 + ½ · 0) =
= – 92,3 кДж/моль.
DH0rВ = (DH0f (H2) + ½ DH0f (О2)) – DH0f (H2О) = (0 + ½ · 0) – (– 285,85) =
= 285,85 кДж/моль.
З наведених розрахунків випливає:
Висновок 1. Якщо вихідні речовини прості, а кінцевий продукт один, то енергетичний ефект процесу дорівнює енергії утворення продукту. Якщо ж простими речовинами є кінцеві продукти, а вихідна речови-на одна, то енергетичний ефект дорівнює енергії розкладу вихідної речовини. При кількох складних кінцевих продуктах чи вихідних речовинах енергетичний ефект процесу відповідній різниці сум ене-ргій DЕ0f чи DЕ0d складних речовин.
ІІ. Використовуючи енергохімічні розрахунки можна визначати енергетичні ефекти ще не вивчених реакцій на за відомими реакціями.
Нехай відомі: С(граф.) + О2(г) = СО2(г); DH0r1 = – 393,98 кДж/моль; (1)
СО(г) + ½О2(г) = СО2(г); DH0r2 = – 283,41 кДж/моль; (2)
Треба визначити DH0r3 реакції: С(граф.) + СО2(г) = 2СО(г); кДж/моль;(3)
З аналізу реакцій (1), (2), (3) одержуємо, що DH0r3 = DH0r1 – 2 DH0r2,
оскільки С(граф.) + О2(г) = СО2(г);
____________ 2СО(г) + О2(г) = 2СО2(г);_______________
С(граф.) + О2(г) – 2СО – О2(г) = СО2(г) – 2СО2(г);
С(граф.) – 2СО(г) = – СО2(г); Þ С(граф.) + СО2(г) = 2СО(г);
Тоді DH0r3 = – 393,98 – 2(– 283,41) = 142,84 кДж/моль
що означає те, що реакція є екзотермічною.
Висновок 1. Комбінуючи відомі реакції так, щоб одержати реакцію неви-вчену слід використовувати ті ж правила комбінування, які викори-стовуються для визначення енергетичних ефектів невивченого про-цесу.
ІІІ. На підставі енергохімічного аналізу можна передбачити склад кінцевих речовин (продуктів) реакції і, навіть, оцінити в них вміст кожної з речовин:
Нехай мають місце два паралельних (альтернативних) процеси:
a A + b B ® 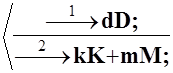
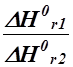 .
.
Очевидно, що у цьому випадку необхідно говорити про ймовірність перебігу процесу шляхами 1 або 2. Значення ймовірностей для різних зна-ків DЕ0r,i, i = 1, 2 подано у таблиці 3.
Таблиця 5.3.
Енергохімічні ймовірності перебігу альтернативних процесів.
| Значення DЕ0r,i,i = 1, 2 | Ймовірності процесу | |
| шляхом 1 | шляхом 2 | |
| DЕ0r,1 <0 DЕ0r,2 <0 | 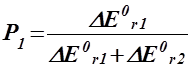
| 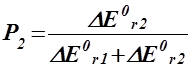
|
| DЕ0r,1 >0 DЕ0r,2 <0 | 
| 
|
| DЕ0r,1 <0; DЕ0r,2 >0 а) ½ DЕ0r,1 ½= DЕ0r,2 б) ½ DЕ0r,1 ½> DЕ0r,2 в) ½ DЕ0r,1 ½< DЕ0r,2 |
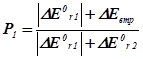
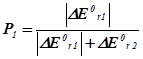
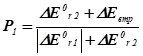
|
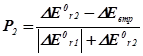
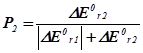
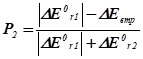
|
Тут DЕ0втр. – втрати енергії, що виділяються у першій реакції у навколишнє середовище.
Тепер, якщо здійснити розрахунки для випадку DЕ0r,1 < 0; DЕ0r,2 < 0 при вихідних речовинах А і В, узятих у стехіометричних співвідношен-нях, т
Нехай, наприклад, А і В узято у стехіометричних співвідношеннях, та нехай ½ DН0r,1 < 0½Þ ½ DН0r,2 > 0½. Тоді Р2 = 2/3, P1 = 1/3. Отже, серед продуктів буде міститися: P1d молів речовини D та P2k й P2m молів речовин K і M.
Висновок 3. Якщо енергетичні ефекти обох процесів від’ємні, то більш інтенсивним буде процес із більшим за модулем значенням цього ефекту. Якщо енергетичні ефекти двох процесів додатні, то більш інтенсивним буде процес із меншим значенням ефекту. Якщо енер-гетичні ефекти двох процесів мають різні знаки, то більш інтенсив-ним буде процес із від’ємним значенням цього ефекту, а на другий процес припадатиме лише та частка енергії, яку йому надасть перший процес.
IV. З термохімічних розрахунків можна знайти значення енергії хімічних зв’язків. При цьому слід розуміти різницю значень істинних і практичних. Енергією зв’язку (істинною) називається приріст (перерахо-ваний на один зв’язок) енергії моля індивідуальної речовини при руйнуванні певного зв’язку в кожній молекулі та віддаленні утворених частинок. Таку енергію з досліду визначити практично неможливо. Прак-тичною енергією є та частка енергії, яка поглинається при повній дисоціації (у перерахунку на даний зв’язок) молекул на вільні атоми.
Нехай потрібно розрахувати енергію зв’язку С – Н використовуючи реакції: С(г) + 2Н2(г) ® СН4(г); DН0r,1 = – 66,99 кДж/моль;
С(т) ® С(г); DН0r,2 = – 69,22 кДж/моль;
Н2(г) ® 2Н(г); DН0r,1 = 431,78 кДж/моль.
Комбінуючи реакції (1) – (3) одержуємо: (4) = (2) – ((1) + (3)):
СН4(г) ® С(г) + 4Н(г); DН0r,4 = + 1654,21 кДж/моль;
Енергії дисоціації на атоми дорівнюють сумам енергій усіх зв’язків у молекулі. Отже DН0r,4 = 4 Е (С – Н) Þ Е (С – Н) = (1654,21 кДж/моль): 4»»413,55 кДж/моль.
Висновок 4. Одержувані значення енергій зв’язків може бути уточнено за рахунок урахування додаткових енергетичних ефектів, окрім дисоці-ації.
IV. Перевіримо експериментально результати розрахунків, викона-них для реакцій (а) та (б) (див. п. І). З розрахунків випливає, що реакція (а) самодовільна (DН0r < 0), а реакція (б) здійсниться, якщо до 1 моля води (18 г) застосувати 285,85 кДж енергії. Вмістимо для початку по 0, 5 моля H2 та Cl2 в замкнену посудину, місткістю в 24,45 л, що відповідає об’ємові 1 моля газу за стандартних умов, на достатньо тривалий термін (1 рік). По завершенні цього терміну виявимо, що вміст HCl у посудині не перевищує 1 ¸ 1,2%, тобто реально реакція не відбулася. Щоб перевірити розрахунки за реакцією (б), візьмемо посудину, місткістю в 36,675 л, що відповідає об’ємові 1,5 моля газу за стандартних умов.
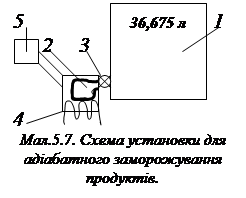





 До цієї посудини 1 (див. мал. 5.7) приєднає-мо за допомогою крану (3) проточну кювету, місткістю 18 см3, заповнену 1 молем води. За допомогою нагрівників передамо воді285,85 кДж теплової енергії. Контролер параметрів (5) при цьому покаже, що вода перетвори-лась на газ при надкритичній температурі Т~ ~ 4500 К та тискові близько 300 МПа.
До цієї посудини 1 (див. мал. 5.7) приєднає-мо за допомогою крану (3) проточну кювету, місткістю 18 см3, заповнену 1 молем води. За допомогою нагрівників передамо воді285,85 кДж теплової енергії. Контролер параметрів (5) при цьому покаже, що вода перетвори-лась на газ при надкритичній температурі Т~ ~ 4500 К та тискові близько 300 МПа.
Щоб визначити склад газу відкриємо кран (3), після чого вміст кювети швидко перейде до посудини (1), розширившись і охолоджуючись до стандартних параметрів. Така операція називається адіабатичним заморо-жуванням. Аналіз “заморожених” продуктів покаже, що це суміш газів Н2 та О2, які на 8 ¸ 9% іонізовані та 30% Н2О. Отже у цьому випадку резуль-тат не відповідає розрахункові, що дозволяє зробити...
Висновок 5. Енергія, за зміною якої передбачають хід процесу, крім змін стану повинна враховувати й умови, у яких відбуваються ці зміни. Це пов’язано з тим, що функції U, H, F та G є функціями стану, а стан у свою чергу залежить від оболонки, у якій перебігає процес. Однак, для того, щоб пов’язати енергії U, H, F та G з певним типом систем, необхідно ознайомитись із основними законами перерозпо-ділу енергії у системі.
ОСНОВНІ ЗАКОНИ ТЕРМОДИНАМІКИ
Сучасна термодинаміка оперує сімома законами. Ми же в межах нашого курсу зупинимось лише на трьох.
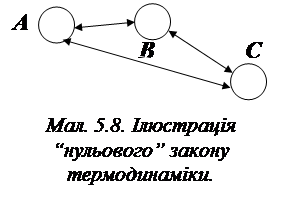 “Нульовий” закон термодинаміки. “Якщо тіло А рівноважне щодо тіла В, а тіло В рівноважне щодо тіла С, то тіла А і С також взаємно рівноважні.”
“Нульовий” закон термодинаміки. “Якщо тіло А рівноважне щодо тіла В, а тіло В рівноважне щодо тіла С, то тіла А і С також взаємно рівноважні.”
З “нульового” закону випливає висновок про те, що якщо у складній системі, що складається з множини об’єктів є хоча б одна пара взаємно нерівноважних, то й уся система є також нерівноважною, та у її об’ємі відбуватимуться процеси доти, доки всі об’єкти не стануть взаємно рівноважними.
Такий процес взаємоурівноважування, який супроводжується не лише фізичними, а й хімічними перетвореннями, як з ускладненням, так і зі спрощенням молекулярної будови називається еволюцією. Остання, у свою чергу, може стати прогресивною, якщо система структурних зв’яз-ків ускладнюється, або регресивною, якщо ця система спрощується.
Так, за даними експериментальної космогонії близько 7,5 мільярдів років тому в області поблизу зірки Бернара відбувся спалах наднової зір-ки. Продукти спалаху утворили газопилову хмару, у якій за 1,5 мільярди років після спалаху зародилось наше Сонце, ще через 1 мільярд років сформувались планети, на одній із яких – нашій Землі ще через 800 млн. років виникло життя, як продукт тривалої прогресивної хімічної еволюції.
Перший закон термодинаміки. Таким чином зовнішній енергетич-ний вплив на систему порушує рівноважні чи динамічні умови, що скла-лися у ній, що змінює енергію системи, яка частково перетворюється у роботу еволюції. Таке міркування дозволило Ю.Р.Майєрові сформулюва-ти сам закон, який є у сутності законом збереження енергії:
“Енергія, що підводиться до системи витрачається на зміну внутрішньої енергії системи та на здійснення нею зовнішньої роботи.”
Математичний запис закону у сучасному тлумаченні:
dЕ = dU + dAex,
де d і d – значення неповного та повного диференціалів. Повний диферен-ціал відповідає величинам, які є функціями стану, тобто задаються набором параметрів системи та не залежать від шляху процесу. Е та Аех, як було показано раніше, залежать від властивостей оболонки, тобто від шляху. Що ж стосується U, то це функція стану, але набір параметрів, не-обхідний для її визначення, залежить від параметрів системи.
Зі сформульованого закону випливають важливі наслідки:
- Нехай dЕ = 0 та dAex = 0 (ізольована система). Тоді dU = 0, тобто U = =const. Однак U = F + TS або U = Ain + TS. Якщо dU =dAin + d(TS) = = 0, то – dAin = d(TS), тобто в ізольованих системах уся внутрішня робота здійснюється лише за рахунок витрати зв’язаної енергії TS.
- Нехай dAex = 0 (замкнена система). Тоді dЕ = dU або dЕ = dAin + d(TS). Отже в замкненій системі уся підведена енергія витрачається лише на зміну внутрішньої енергії U. При цьому на відміну від попе-реднього випадку значення dAin та d(TS) є однозначними.
- Нехай dЕ = 0 (адіабатна система). Тоді dU + dAex = 0 або – dU = dAex чи dAin + dAex = – d(TS), тобто dAt = – d(TS). Отже в адіабатній системі вся робота здійснюється за рахунок зв’язаної енергії.
- Нехай dЕ ≠ 0 та dAex ≠ 0 (відкрита система). Тоді dЕ = dН або dЕ = = dG + d(TS) = dAt + d(TS), звідки dAt =dЕ – d(TS), тобто у відкритих системах уся підведена енергія витрачається на здійснення повної роботи та зміну зв’язаної енергії. При чому dAt і d(TS) – однозначні.
Подальше тлумачення одержаних наслідків можливе тільки після вияс-нення сенсу зв’язаної енергії TS.
Другий закон термодинаміки. Другий закон був уперше сформу-льований Р.Клаузіусом у 1854 році, однак і досі не стихають суперечки щодо його сутності. Сутність же зводиться до того, що закон пояснює, у якому напрямку перепливає енергія та що при цьому з нею відбувається.
На сьогодні відомо близько 80 формулювань другого закону, однак, якщо формулювань багато, то жодне з них не є повним і не здатне відоб-разити всю багатоманітність розглядуваних явищ. За таких обставин мож-на подати оригінальне визначення, що синтезує узагальнюючу сутність вищезазначених визначень:
“Будь-який тип енергії, самодовільно (спонтанно) поширюючись від більшого значення свого потенціалу до меншого частково витрачається на виконання роботи, а частково розсіюється у вигляді тепла”.
При всіх недоліках даного визначення, воно відображує ряд точно встановлених фактів:
- будь-який тип роботи, перетворення, зосередження чи нагромаджен-ня енергії здійснюється одним і тим же процесовим ансамблем сис-теми;
- будь-яка робота є спрямованою дією, яку може бути виконано лише упорядкованим потоком енергії, а не енергією, хаотично розпоро-шеною в об’ємі статистичної системи;
- будь-яка робота супроводжується виділенням тепла, пропорційно здійсненній роботі, при чому це тепло розсіюється у довкіллі, чи нагромаджується системою у вигляді зв’язаної енергії (TS);
Таким чином, другий закон термодинаміки дозволяє одержати відповідь, як початково хаотичний процесовий ансамбль перетворити в упорядкований, спрямовані (самодовільні) потоки енергії якого здатні здійснити роботу (несамодовільний процес) і далі законсервувати енер-гію, вже не придатну для здійснення роботи у хімічних зв’язках. Це об’єднання самодовільних і несамодовільних процесів у єдину дію дозво-ляє визначити вектор еволюції будь-якої з відомих на сьогодні систем.
Дійсно, хаотична (теплова) поведінка будь-якої з частинок ансамблю оборотна. Так для броунівських стрибків є рівноймовірним будь-який за напрямком вектор; амплітуди коливань атомів у вузлах кристалічної ре-шітки симетричні відносно рівноважного стану. В цей же час тепло поши-рюється від високотемпературних зон до низькотемпературних, від біль-шої амплітуди коливань до меншої. Дифузія йде від більшого значення концентрації переношуваної маси до меншої. Вода тече з гори додолу і ніколи самодовільно навпаки.
Отже, система, де здійснена робота переносу тепла маси, електрич-ного заряду, спрямованого хімічного процесу, тощо, повинна бути неод-норідною, із просторовим розподілом високопотенційних і низькопотен-ційних підсистем. У таких системах енергія, самодовільно перепливаючи від високого потенціалу до низького несамодовільно здійснює роботу переносу чи перетворення енергії та знецінюється з точки зору щодо подальшої здатності до виконання роботи. Окрім того тертя напрямлених необоротних потоків та їхнього хаотичного оточення додатково перетво-рює енергію в тепло, розсіювань у навколишньому середовищі.
Однак, кількість дисипованої енергії, рівно як і виконуваної роботи, не безмежні. Потенціал використовуваної енергії не може опуститися нижче потенціалу навколишнього середовища. Таким чином, вихідна різниця потенціалів (ΔТ, Δр, ΔV, ΔC, тощо) обмежує як здійснювану ро-боту так і дисиповану енергію, у тому числі й нагромаджену в утворених внаслідок процесу зв’язках.
Математично кількість знеціненої, дисипованої енергії оцінюється параметром S – ентропією: S ≥ E/T або dS ≥ δE/T, де 1/Т є інтегруючий множник, що дозволяє перевести неповний диференціал δE у повний dS. Знак “дорівнює” (“=”) у цих рівняннях відноситься до оборотних проце-сів, а знак “>” до систем із необоротними явищами, тобто до всіх реаль-них систем. Якщо Е = Еt – Евтр ., де Е, Еt та Евтр відповідно корисна, повна (визначена різницею потенціалів) та втрачена внаслідок необорот-ності енергія, то dS = δEt /T, але 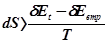 .
.
ІДЕНТИФІКАЦІЯ ТИПІВ СИСТЕМ, ЇХНІХ ХАРАКТЕРИСТИЧНИХ ФУНКЦІЙ ТА ПРИРОДНІХ ПАРАМЕТРІВ
З усього вищезазначеного випливає, що для кожного типу системи існує власна характеристична функція, за значенням якої можна судити про поведінку всієї системи (про самодовільність процесу про умови його перебігу, про ефекти, що цей процес супроводжують, тощо). У якості таких функцій виступають DU, DH, DF та DG, які відповідають різниці цих енергій у кінцевому та початковому станах. Параметри цих функцій називаються природними.
Підставляючи dS ≥ δE/T у рівняння першого закону одержуємо:
ТdS ≥ dU + δAex.
Якщо δE = 0, то й ТdS = 0, тобто S = const, що справедливо для ізольованих і адіабатних систем. Якщо ж δE ≠ 0, (системи відкриті й замкнені), то Т = const.
Нехай робота системи At = Fl, то δAt = Fdl + ldF = Aex + Ain. Якщо Aex = 0 (системи ізольовані та замкнені), то l = constAex = Fdl = 0; F ≠ 0. Для систем же адіабатних та відкритих F = const. Так для систем, що здійснюють роботу розширення F ≡ р, а Δl ≡ ΔV. Для систем, що здійснюють кілька видів робіт 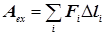 .
.
Взаємозв’язки типів систем, їхніх характеристичних функцій та па-раметрів, подано на мал. 5.9. та у таблиці 5.4.
 Таблиця 5.4.
Таблиця 5.4.
Взаємозв’язок типів систем
із їхніми характеристичними функціями
та природними параметрами.
 Тип системи Тип системи
| Параметри | Характерис-тична функція | |
| природні | вільні | ||
| Ізольована | S, V | p, T | dUS,V |
| Замкнена | T, V | p, S | dFT,V |
| Адіабатна | S, p | V, T | dHS,p |
| Відкрита | T, p | V, S | dGT,p |
Тепер можна стверджувати, що, якщо, наприклад DН0p < 0, то ця реакція можлива та буде перебігати самодовільно, але тільки в адіабатних системах. Для усіх інших систем знання DН0р необхідне, але недостатнє, оскільки DUр = DHр – Aex; DFр = DНр – Aex – TΔSp; DG0р = DН0р – TΔSp.
ЕНТРОПІЯ
Раніше вже відзначалося, що ентропія – це функція стану, що дорів-нює сумі приведених енергій, поглинутих системою при виконанні проце-су: 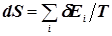 . Припускається, що всю цю енергію приведено до одного потенціалу – температури середовища, оскільки температура є потенціал тепла, у яке трансформується будь-який вид поглинутої енергії. Тому в ряді випадків приведена енергія може мати вигляд: (ξі · δЕі)/ T, де ξі – коефіцієнт перерахунку потенціалу даного типу енергії (наприклад елек-тромагнітної) у температуру.
. Припускається, що всю цю енергію приведено до одного потенціалу – температури середовища, оскільки температура є потенціал тепла, у яке трансформується будь-який вид поглинутої енергії. Тому в ряді випадків приведена енергія може мати вигляд: (ξі · δЕі)/ T, де ξі – коефіцієнт перерахунку потенціалу даного типу енергії (наприклад елек-тромагнітної) у температуру.
З того, що будь-яка енергія перетворюється у теплоту з потенціалом Т випливає:
- ентропія є величина статистична, тобто як не може бути температу-ри чи тиску однієї частинки, так і ентропія відноситься лише до ан-самблю частинок;
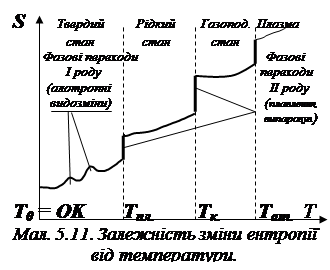
- у рівновазі, характеризованій потенціалом Т0 система стає однорід-ною, локальні різнопотенціальні підсистеми розчиняються в об’ємі системи, напрямлені потоки енергії (які виконують роботу) зника-ють, замінюючись статистично рівномірно характеризованим розпо-ділом енергії; таким чином, природний рух системи до рівноваги – це рух до хаосу в розподілі енергії, зниженню роботоспроможності системи та зростання її ентропії (див. мал. 5.10);
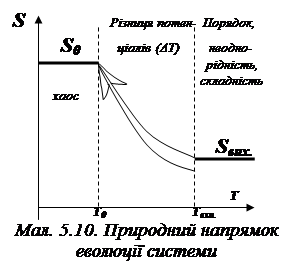
-  зі зростанням температури потенціал системи Т зростає відносно потенціалу середовища Т0; у системі зв’язки рвуться, кінетична ене-ргія частинок зростає, система хаотизується, її ентропія зростає, але й зростає роботоспроможність відносно навколишнього середовища (див. мал. 5.11);
зі зростанням температури потенціал системи Т зростає відносно потенціалу середовища Т0; у системі зв’язки рвуться, кінетична ене-ргія частинок зростає, система хаотизується, її ентропія зростає, але й зростає роботоспроможність відносно навколишнього середовища (див. мал. 5.11);
 |
Це удаване протиріччя: хаотизація при Т = Т0 збільшує ентропію при зниженні роботоспроможності, але при Т > Т0 зростання ентропії під-вищує роботоспроможність системи, було пояснено Л.Больцманом на підставі статистичного характеру ентропії. З одержаного ним рівняння
S = – k · ln(P) = – (R/NA)ln(P),
де k = R/NA – стала Больцмана; R = 8,314 Дж/(моль · К) – універсальна газова стала; NA = 6,02 · 1023 моль-1 – число Авогадро. Для нас найбільш важливим є число P. P – це ймовірність того, що з N вільних та Nзв зв’язаних частинок можливе виникнення стану Wi при W0 можливих станів. Тоді: Pроб. (Т > Т0) = W/W0 = 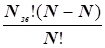 ;
;
Pнероб. (Т = Т0) = W/W0 = 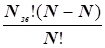 .
.
Очевидно, що за порядком обидві ймовірності роботоспроможного та нероботоспроможного станів майже однакові, що й забезпечує їм однакове значення ентропії, як роботоспроможної – нерівноважної, так і нероботоспроможної – рівноважної систем.
Інтерпретація результатів розрахунку змін ентропії.
Оцінити знак зміни ентропії ряду процесів можна навіть без розра-хунків. Для цього необхідно лише пам’ятати, що при хаотизації системи, тобто при її русі від порядку до хаосу ΔS > 0, а якщо у протилежному напрямку, то ΔS < 0. Наприклад: Fe(т) → Fe(р) – процес плавлення. Хаос у рідині більше, тобто в даному разі напрямок зміни порядок → хаос чи ΔS > 0. Інший приклад: С(т) + СО2(г) → 2СО(г). У цьому процесі у лівій частині рівняння один моль твердої та один моль газоподібної речовин, а у правій частині 2 молі газоподібної. Також очевидно, що процес іде до хаосу, тобто ΔS > 0. Ще приклад: HCl(р) + NaOH(р) → NaCl(р) + H2O(р). Ліворуч і праворуч маємо по два молі речовин у рідкій фазі (розчині), але ліворуч обидві речовини добре дисоційовані, а праворуч вода практично не дисоціює. У такому разі можна твердити, що система впорядковується, тобто ΔS < 0. У подібних оцінках слід перед усім брати до уваги фазовий склад реагентів, точніше ті речовини, у яких рухливість частинок вище. Тим не менш навіть оцінки можуть бути помилковими.
Для розрахунків використовують базований на той же, базований на законі Геса, метод, використання якого вже було продемонстровано. При цьому слід пам’ятати, що ентропія утворення S0f [Дж/(моль · К)] чи Sf [Дж/К] навіть простих, навіть дуже твердих речовин більше нуля.
І. Нехай має місце реакція: a A + b B ® d D + e E, де A, B, D та E – по-значення хімічних речовин, а a, b, d та e – стехіометричні коефіцієнти при них, а також відомі ентропії утворення за стандартних умов: S0f,A, S0f,B, S0f,D та S0f,E. Тоді ентропія реакції ΔS0r = (d S0 f,D + e S0 f,E) – (a S0 f,A + b S0 f,B). За знаком результат ΔS0r може бути: а) > 0 – система спрощується;
б) = 0 – система структурно незмінна;
в) < 0 – система ускладнюється;
ІІ. Потрібно порівняти стабільність чи хімічну активність речовин А і В, якщо відомо, що S0f,A > S0f,B. Речовини будуть тим стабільніше чим менше S0f, і тим активніше, чим вище S0f, отжебільш активною буде речовина А, а більш стабільною – речовина В.
ІІІ. Раніше відзначалось, що в ізольованій та адіабатній системах уся робота здійснюється за рахунок зв’язаної енергії. При цьому: dAin = dAt = – d(TS), де d(TS) = TdS + SdT.
Однак, dAin відповідає значенню dU = 0.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 613; Нарушение авторских прав?; Мы поможем в написании вашей работы!