Математическое ожидание и дисперсия генеральной совокупности непрерывной случайной величины

Математическим ожиданием непрерывной случайной величины Х, значения которой принадлежат отрезку [ a,b ], называется определенный интеграл:

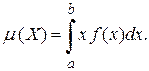(4.16)

Если значения случайной величины принадлежат интервалу то

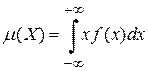. (4.17)

Дисперсией непрерывной случайной величины Х, значения которой принадлежат отрезку [a,b], называют математическое ожидание квадрата ее отклонения:

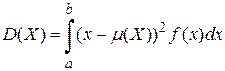^.. (4.18)

Если значения случайной величины Х принадлежат всей числовой оси, тогда дисперсия равна:

_.

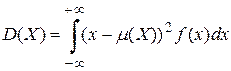Среднеквадратическое отклонение равно

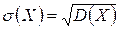. (4.19)

Все свойства математического ожидания и дисперсии дискретной случайной величины сохраняются и для непрерывной случайной величины.

Нормальный закон распределения (закон Гаусса)

Нормальный закон играет особую роль в науке и технике. Это наиболее часто встречающийся закон распределения при решении практических задач обработки экспериментальных результатов. Главная его особенность заключается в том, что он описывает случайную величину, на которую влияют многие случайные факторы, причём вклад каждого из них мал. Каждый из них скрыт от исследования, а экспериментатор, следящий за состоянием процесса в целом, наблюдает лишь суммарное действие этих факторов. Именно такая ситуация возникает чаще всего при измерениях в естественных науках и технике. При измерении таких величин возникают неконтролируемые погрешности (ошибки) поэтому графическое изображение этого закона часто называют «кривой ошибок», а его интегральную форму − «интегралом ошибок». Нормальный закон играет особую роль и с точки зрения математической статистики, что следует из центральной предельной теоремы, согласно которой нормальный закон является предельным законом, к которому приближаются другие.

Распределение вероятностей называется нормальным, если оно описывается дифференциальной функцией (плотностью вероятности) вида:

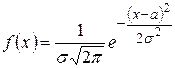, (4.30)

где: а - математическое ожидание, s - среднеквадратическое отклонение. Если случайная величина Х распределена по нормальному закону, то пишут Х Î N (a,s). График нормальной плотности распределения вероятности представлен на рис.4.7.

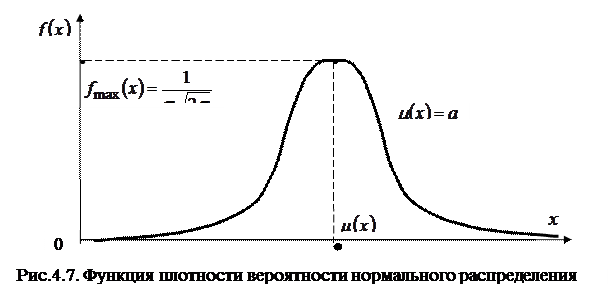
Нормальный закон распределения часто называют законом Гаусса. Функция 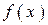определена при любых значениях х. Кривая распределения симметрична относительно прямой 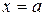, асимптотически приближается к оси абсцисс, так как 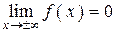. При 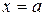функция 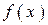имеет максимальное значение, а именно .

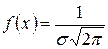Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок, равна:

. (4.31)

Пользуясь заменой переменных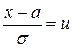, получим формулу для вычисления вероятности попадания случайной величины на заданный участок:

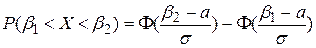, (4.32)

где 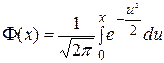-интегральная функция Лапласа. Для нахождения этого интеграла используют таблицу. Функция Лапласа имеет следующие свойства: 1) 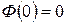, 2) 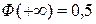, 3)Функция Лапласа нечетная, т.е..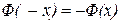, 4) При x>5 принимают .

Вероятность попадания случайной величины Х на участок длины 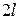, симметричный относительно центра рассеивания 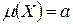вычисляется по формуле:

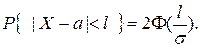(4.33)

С помощью функции Лапласа интегральная функция нормального распределения выражается следующим образом:

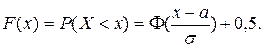
(4.34)

Рассмотрим следующий пример: Длина детали, изготовляемой автоматом, представляет собой случайную величину, распределенную по нормальному закону, причем 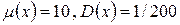. Найти вероятность брака, если допустимые размеры детали должны быть 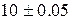. Используя формулу (4.33), можно рассчитать вероятность отсутствия брака, то есть вероятность попадания в допустимый интервал 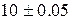.Вероятность брака есть вероятность непопадания в указанный интервал. Поскольку оба этих события составляют полную группу несовместимых событий, а вероятность полной группы равна 1,выражается формулой: вероятность брака равна

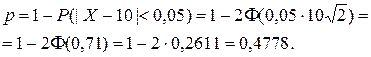
Правило трех сигм. Вычислим вероятность попадания случайной величины Х на симметричный участок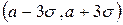

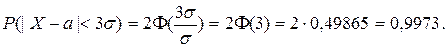
Это означает, что попадание значения случайной величины в промежуток 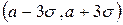имеет вероятность 99,73%, то есть является практически достоверным событием.

Дата добавления: 2013-12-13