Доверительный интервал для математического ожидания при известной дисперсии генеральной совокупности

Пусть случайная величина X (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия D (X) = s ² (s > 0). Из генеральной совокупности (на множестве объектов которой определена случайная величина) делается выборка объема M. Выборка x ₁, x ₂,..., x_M рассматривается как совокупность M. независимых случайных величин, распределенных так же как X. В математической статистике доказывается, что выборочное среднее является случайной величиной, которая также распределена по нормальному закону.

Обозначим неизвестное математическое ожидание случайной величины через a 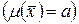и поставим задачу определить доверительный интервал 2для a, если известны доверительная вероятность 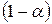и объём выборки M.

Запишем вероятность попадания значения в интервал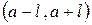

.

Выборочное среднее распределено по нормальному закону с дисперсией . Подсчитаем вероятность попадания в интервал от до 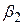по формуле ((4.31), приняв ,

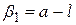
. (4.38)

Для того, чтобы свести данный интеграл к интегралу Лапласа, проведём замену переменно 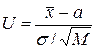, и получим формулу для вычисления вероятности попадания случайной величины на заданный участок (см.выражение (4.32)):

, (4.39)

которую можно переписать в виде

. (4.40)

Будем обозначать доверительную вероятность 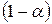буквой 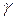. Доверительная вероятность представлена графически на рис.2.8. При построении интервальных оценок, её значения заданы. Используем соотношение

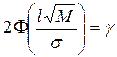или , (4.41)

которое, с учётом замены переменной перепишем .Для любого g Î[0;1] можно по таблице найти такое число , что .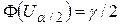

Это число иногда называют квантилем. Наиболее употребляемые квантили представлены в таблице 4.7

Таблица 4.7

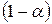
	0,90	0,95	0,975	0,995	0,999
	1.282	1.645	1.960	2.576	3. 09

Теперь, из равенства 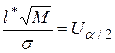, определим значение 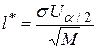. Заменяя в неравенстве (4.40) на , раскрывая это неравенство относительно a и учитывая, что функция Лапласа в данном случае равна γ, окончательный результат можно представить в виде

. (4.42)

Смысл последнего выражения заключается в следующем: с вероятностью g выборочное среднеенаходится в доверительный интервале

Пусть, например, имеется генеральная совокупность, распределенная по нормальному закону с генеральной дисперсией, равной σ² = 6.25. Произведена выборка объема M = 27 и получено выборочное среднее значение характеристики = 12. Найдём доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью g =0.995.

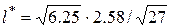Сначала, используя таблицу 4.7 находим, что для доверительной вероятности g =0.995 =2.58. Тогда, значение = 1.24. Доверительный интервал для математического ожидания определяется соотношением (12–1.24 < a < 12+1.24).Таким образом, с вероятностью 99.5 %, можно утверждать, что значение математического ожидания 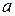лежит в интервале (10,76; 13,24).

Дата добавления: 2013-12-13