Вероятности

Интервальные оценки параметров нормального распределения

Пусть Х Î N (a,s), причем а и s неизвестны. Для нахождения точечных оценок а и s из генеральной совокупности извлечена выборка объемом M. Пусть на основании этой выборки найдены точечные несмещенные оценки неизвестных параметров а и s по формулам (4.21) и (4.28)

Точечные оценки, найденные по выборке объемом M, не позволяют непосредственно ответить на вопрос, какую ошибку мы допускаем, принимая вместо точного значения неизвестного параметра а или s его приближенные значения .

Поэтому во многих случаях выгоднее пользоваться интервальной оценкой, основанной на определении некоторого интервала, внутри которого с определенной вероятностью находится неизвестное значение параметра а (или s).

Пусть найденная по результатам выборки объема M статистическая характеристика 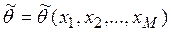является точечной оценкой неизвестного параметра q. Чем меньше разность 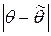, тем лучше качество оценки, тем она точнее. Таким образом, положительное число характеризует точность оценки

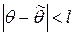. (4.35)

Однако статистический метод не позволяет категорически утверждать, что оценка удовлетворяет неравенству (4.35) в смысле математического анализа. Можно только говорить о вероятности (1-a), с которой это неравенство выполняется, где– вероятность того, что не попала в указанный интервал.

Доверительной вероятностью оценки называют вероятность γ = (1-a) выполнения неравенства . Обычно доверительная вероятность оценки задается заранее. Наиболее часто полагают γ = (1-a) = 0,95; 0,99; 0,9975. Доверительная вероятность точечной оценки показывает, что при извлечении выборки объема M из одной и той же генеральной совокупности в (1-a) 100% случаях параметр q будет накрываться данным интервалом. При выборе доверительной вероятности нужно придерживаться компромисса между значением этой вероятности и величиной доверительного интервала поскольку, чем выше задана доверительная вероятность, тем больше получается доверительный интервал. Тогда высокая достоверность оценки обесценивается низкой её точностью.

Пусть вероятность того, что равна (1-a)

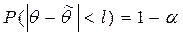. (4.36)

Преобразуем формулу (4.36)

. (4.37)

Последняя формула показывает, что неизвестный параметр q заключен внутри интервала с вероятностью . Этот интервал называется доверительным.

Итак, доверительный интервал накрывает неизвестный параметр q с заданной надежностью (1-a).

В практических приложениях важную роль играет длина доверительного интервала. Чем меньше длина доверительного интервала 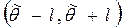, тем точнее оценка.

Из формулы (4.37) видно, что длина доверительного интервала равна 2. Длина доверительного интервала 2определяется двумя величинами: доверительной вероятностью (1-a) и объемом выборки M. Таким образом, , (1-a) и M тесно взаимосвязаны и, задавая определенные значения двум из них, можно определить величину третьей.

Дата добавления: 2013-12-13