Поздовжні коливання стержня. Виведення хвильового рівняння

Лекція 2 Поздовжні коливання стержня

Контрольні запитання

1.1 Що є предметом математичної фізики?

1.2 За допомогою яких математичних засобів моделюються фізичні задачі та явища, пов’язані з температурними, хвильовими та іншими процесами?

1.3 Означення диференціального рівняння з частинними похідними, його порядок.

1.4 Що є розв’язком диференціального рівняння з частинними похідними і від чого він залежить?

1.5 Чим відрізняється загальний розв’язок диференціального рівняння з частинними похідними від загального розв’язку диференціального рівняння?

1.6 Які фізичні процеси та явища описуються канонічними диференціальними рівняннями гіперболічного (еліптичного, параболічного) типу?

1.7 Як звести диференціальне рівняння з частинними похідними, яке є лінійним відносно похідних другого порядку, до канонічного типу?

1.8 Мета зведення диференціального рівняння з частинними похідними до канонічного типу.

1.9 Класифікація диференціального рівняння з частинними похідними другого порядку.

1.10 Як канонічний вид диференціального рівняння другого порядку з частинними похідними залежить від знаку визначника 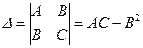та дискримінанта D=В²−АС?

Розглянемо задачу про поздовжні коливання, які виникають у стержні під час його розтягу або стиску внаслідок прикладених зусиль.

При виведенні рівняння, яке описує такі коливання, зробимо ряд припущень відносно геометричного та фізичного станів стержня. Нехай стержень, як тіло циліндричної або призматичної форми, буде задовольняти наступним умовам:

1) стержень прямолінійний завдовжки l;

2) поперечний переріз є сталим, тобто його площа S =const;

3) стержень однорідний, тобто густина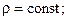

4) стержень пружний, тобто мова йде про пружні коливання, коли має місце закон Гука і немає залишкових деформацій (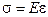, де 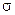– нормальне напруження, 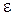– відносна поздовжня деформація, 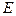– модуль Юнга, );

5) стержень ізотропний, тобто властивості матеріалу, з якого виготовлено стержень, у всіх напрямках однакові;

6) коливання малі;

7) зовнішні сили, якщо вони є, діють вздовж осі стержня;

8) в результаті коливань поперечні перерізи залишаються перпендикулярними до осі стержня.

Розглянемо стержень, вздовж осі якого спрямуємо вісь 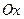(рис. 2.1). Виділимо довільний елемент стержня .

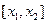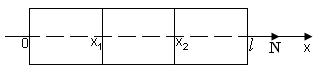
Рис. 2.1 – Стержень з виділеним довільним елементом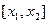

Прикладемо до стержня деяку осьову, наприклад, розтягуючу силу 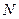, під дією якої поперечні перерізи стержня змістяться, кожний на свою величину.

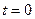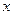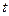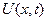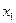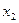Припустимо, що в деякий момент часу, який приймаємо за початковий (), силу знято. Тоді у стержні виникають поздовжні коливання, оскільки, будучи пружним, він намагається повернутися у свій початковий стан. Нехай у результаті коливань кожний переріз в момент часу зміститься на деяку величину . Тоді переріз , зміститься на величину , а – на 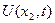, а виділений елемент 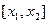займе положення 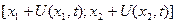і видовжиться на величину

.

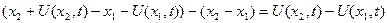Це є абсолютним видовженням. Позначимо початкову довжину виділеного елемента через 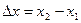і знайдемо відносну деформацію 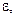як границю відношення абсолютного видовження до довжини елемента, коли ця довжина прямує до нуля:

.

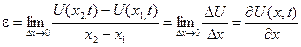Очевидно, що відносна деформація – величина безрозмірна.

Для виведення рівняння, яке описує коливальний процес скористаємося другим законом Ньютона [1], згідно якого сума всіх діючих на рухомий об’єкт сил дорівнює добутку маси на прискорення. Розглянемо сили, які можуть діяти на виділений елемент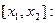

1) Внутрішні сили 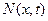, які згідно із законом Гука для будь-якого перерізу x і будь-якого часу t

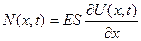. (2.1)

Отже, у перерізі 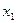діє сила 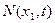, а у перерізі 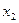– сила 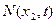. Таким чином, на виділений елемент діє внутрішня сила

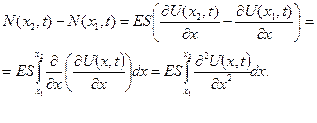(2.2)

2) Зовнішні сили, які за нашим припущенням діють вздовж осі стержня. Позначимо через f (x,t) величину цієї сили, віднесену до одиниці об’єму (інтенсивність зовнішніх сил). Тоді на елементарний об’єм 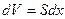діє сила 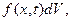а на виділений елемент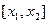

. (2.3)

3) Сила інерції, яка діє на елементарний об’єм 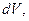дорівнює

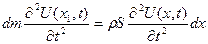. (2.4)

А для виділеного елемента 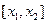ця сила дорівнює

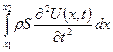. (2.5)

Згідно із другим законом Ньютона маємо:

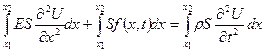, або

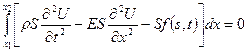. (2.6)

Вважаємо, що підінтегральна функція неперервна на довільно вибраному елементі 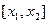. Тоді, за основною лемою математичної фізики (якщо 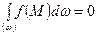для будь-якої області 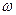, що належить розглядуваній області 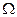, і якщо 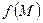– неперервна функція точки М, то 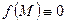в 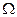[3]) підінтегральний вираз буде дорівнювати нулю, отже,

/

.

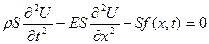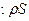
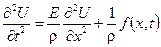Введемо позначення

.

Тоді

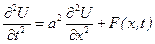, . (2.7)

Одержане рівняння називається хвильовим рівнянням, яке описує поздовжні коливання у стержні.

Проаналізуємо це рівняння. Шукана функція U(x,t) – це зміщення перерізу 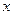в будь-який момент часу.

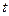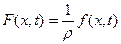– характеризує наявність зовнішніх сил.

Якщо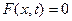, то хвильове рівняння

, (2.8)

описуватиме власні поздовжні коливання у стержні.

Якщо 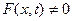, то хвильове рівняння описуватиме вимушені коливання.

Визначимо вільний член 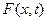у випадку врахування сили тяжіння. При цьому стержень розташований вертикально вздовж осі 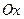, напрямленої донизу. Середня інтенсивність сили тяжіння для будь-якого елемента стержня довжиною дорівнює відношенню ваги 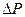цього елемента до його об’єму 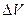: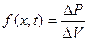. А у перерізі :

.

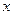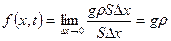Отже, 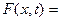g.

Хвильове рівняння для важкого стержня:

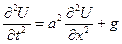, . (2.9)

Дата добавления: 2013-12-14