Постановка задачі математичної фізики про поздовжні коливання стержня

Для повного визначення поздовжніх коливань стержня одного хвильового рівняння недостатньо. Із фізичних міркувань випливає [2], що для того, щоб однозначно описати коливальний процес необхідно додатково задати величини зміщення 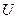перерізів стержня і швидкості 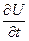в початковий момент часу (початкові умови) і режим на кінцях стержня (крайові умови).

Отже, постановка задачі про поздовжні коливання стержня складається з хвильового рівняння (диференціального рівняння 2-го порядку для функції двох змінних 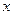і 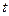) та двох початкових і двох крайових умов.

Початкові умови (П.У.) характеризують стан стержня в початковий момент часу :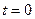

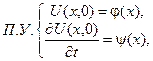(2.10)

де – зміщення перерізу х в момент часу 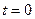(епюра зміщень); – швидкість точок перерізу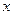стержня при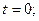 та – задані функції.

Крайові умови (К.У.) показують, що відбувається на кінцях стержня під час коливань.

Розглянемо різні види граничних умов:

1) Нехай один кінець стержня закріплений жорстко, а другий – вільний (Рисунок 2.2).

Якщо вважати, що нерухомим кінцем стержня є 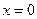, а вільним 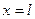, то:

Рисунок 2.2 – Стержень, один з кінців якого закріплений, а другий – вільний

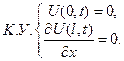(2.11)

Дійсно так, бо для закріпленого кінця характерним є те, що зміщення його весь час дорівнює нулю, а для вільного кінця – те, що у перерізі 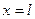пружна сила . Отже, . Звідси

2) Нехай один кінець стержня закріплений жорстко, а до вільного кінця (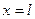 ) прикладено силу P (Рисунок 2.3). Тоді маємо:

Рисунок 2.3 – Один кінець стержня жорстко закріплений, а на другий – діє сила Р

(2.12)

3) Нехай обидва кінці стержня жорстко закріплені

(Рисунок 2.4). Тоді:

Рисунок 2.4 – Обидва кінці стержня жорстко закріплені

(2.13)

4) Нехай один кінець стержня (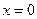) жорстко закріплений, а на другому кінці (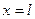) має місце в’язкий опір з коефіцієнтом в’язкості(Рисунок 2.5).

Тоді, враховуючи, що сила в’язкого опору пропорційна швидкості руху, і записуючи умову рівноваги на правому кінці, маємо:

Рисунок 2.5 – На правому кінці стержня має місце в’язкий опір

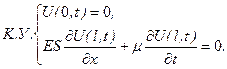(2.14)

5) Нехай один кінець стержня (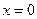) жорстко закріплено, а до другого (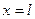) приєднано вантаж маси М (Рисунок 2.6). Тоді на цьому кінці виникає сила інерції, яка дорівнює добутку маси вантажу на прискорення руху. Записуючи умову рівноваги на кінці маємо:

Рисунок 2.6 – Один кінець стержня жорстко закріплено, а до іншого приєднано вантаж маси М

(2.15)

6) Нехай один кінець стержня (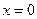) жорстко закріплено, а другий (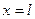) – пружно: до цього кінця прикріплено пружину з жорсткістю с (Рисунок 2.7). Оскільки вважається, що сила натягу пружини прямо пропорційна зміщенню, то, записуючи умову рівноваги на кінці маємо:

Рисунок 2.7 – Один кінець стержня закріплено жорстко, а другий – пружно

(2.16)

Задача 2.1 Стержень довжини l, один кінець якого жорстко закріплено, перебуває у стані спокою. У деякий момент часу (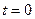) до його вільного кінця прикладено силу Q, напрямлену вздовж осі стержня. Сформулювати задачу про поздовжні коливання стержня.

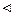Щоб поставити задачу, потрібно записати диференціальне рівняння, яке моделює даний фізичний процес, а також початкові та крайові умови, які відображають специфіку цієї задачі. Вважаємо, що стержень перебуває у стані спокою. Коливання виникають у момент прикладання сили Q до вільного кінця, отже,

,

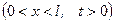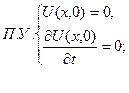
Розв’язком цієї задачі є функція 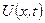класу .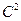

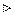
Задача 2.2 Поставити задачу про поздовжні коливання стержня, один кінець якого жорстко закріплено, а до вільного кінця прикладено силу P, причому в момент часу 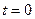дія сили раптово припиняється.

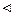Як і в попередній задачі вважаємо, що в початковий момент часу стержень перебуває у стані спокою. Сила P до її зняття встигла розтягнути стержень – кожний переріз х на свою величину U. Знайдемо її:

, .

Зінтегрувавши останнє рівняння по змінній х у межах від 0 до х, отримаємо:

. Тоді постановка задачі має вигляд:

,

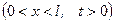Зауважимо, що тут коливання виникають у момент зняття сили Р. Розв’язком цієї задачі є функція 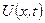класу .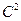

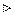
Задача 2.3 Верхній кінець вертикального підвішеного важкого стержня прикріплено до стелі ліфта, який вільно падає, причому досягши швидкості V, він раптово зупиняється. Поставити задачу про поздовжні коливання стержня.

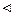Тут коливання виникають у момент зупинки ліфта, коли раптово починає діяти сила тяжіння. Сила тяжіння відноситься до зовнішніх сил і тому її вплив проявиться в диференціальному рівнянні, отже,

,

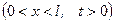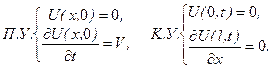
Розв’язком цієї задачі є функція 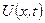класу .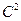

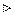
Дата добавления: 2013-12-14