Вольт-амперные характеристики линейного емкостного элемента описываются дифференциальными или интегральными линейными уравнениями (1.22), (1.25)

Вывод

Если напряжение на зажимах емкости на изменяется во времени, то ток емкости равен нулю. Таким образом, сопротивление емкости постоянному току бесконечно велико.

Используя выражение (1.22), находим зависимость напряжения емкости от тока:

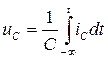(1.23)

Чтобы учесть все возможные изменения заряда емкости и, следовательно, напряжения u_c, имевшие место до рассматриваемого момента времени t, интегрирование ведется начиная с 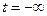, причем принимается, что при 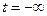напряжение на зажимах емкости равно нулю.

Пусть наблюдение процессов в емкости началось в момент времени t=t_o, тогда напряжение емкости в начальный момент:

. (1.24)

Разбивая интеграл (1.23) на два:

.

и используя выражение (1.24), определим напряжение емкости в произвольный момент времени t:

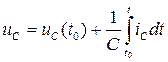. (1.25)

Мгновенная мощность емкости P_C определяется произведением мгновенных значений тока i_c и напряжения u_c:

. (1.26)

Из выражения (1.26) следует:

1) если напряжение емкости (см. рис. 1.9) положительно (т.е. его направление совпадает с условно-положительным направлением, указанным стрелкой) и продолжает возрастать, то мгновенная мощность емкости в соответствии с (1.26) будет положительной; в этом случае энергия поступает в емкость, т.е. она заряжается;

2) если напряжение u_c>0 и убывает, т.е. du_c/dt<0, то мгновенная мощность емкости отрицательна; емкость при этом разряжается, т.е. отдает накопленную энергию во внешнюю цепь.

Энергия, запасенная в емкости:

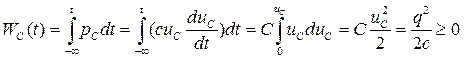(1.27)

При интегрировании в формуле (1.27) произведена замена переменных, причем учтено, что в момент времени t напряжение емкостного элемента равно u_c, а при напряжение u_c=0.

Дата добавления: 2013-12-14