Образовательное учреждение высшего. Ток источника тока и напряжение источника напряжения являются параметрами идеализированных активных элементов подобно тому

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

Ток источника тока и напряжение источника напряжения являются параметрами идеализированных активных элементов подобно тому, как сопротивление, емкость и индуктивность являются параметрами одноименных идеализированных пассивных элементов.

Рис. 1.15

Если к внешним выводам источника тока подключить нагрузку R _н. (рис. 1.15), то, согласно (1.9), (1.11), напряжение на нагрузке и выделяемую в ней мощность можно определить из выражении:

; . (1.30)

С увеличением R _н, напряжение на нагрузке и выделяемая в ней мощность неограниченно увеличиваются, поэтому источник тока, так же как и источник напряжения, является источником бесконечной мощности.

Зависимость тока источника тока от напряжения имеет такой же вид, как и зависимость напряжения источника напряжения от тока, поэтому эти источники являются дуальными элементами.

Предельный случай когда R _н.=(режим холостого хода источника), исключается из рассмотрения, так как при этом возникает противоречие. С одной стороны, при R _н.=напряжение на выходе источника бесконечно велико, цепь нагрузки фактически разорвана и ток источника должен равняться нулю, с другой стороны, в соответствии с определением источника тока ток источника не зависит от напряжения на его зажимах и при u =так же должен равняться j(t).

Таким образом, идеальный источник тока можно рассматривать как источник энергии с бесконечно малой внутренней проводимостью (бесконечно большим внутренним сопротивлением).

5.3 СХЕМЫ ЗАМЕЩЕНИЯ РЕАЛЬНЫХ ИСТОЧНИКОВ

Идеальные источники тока и напряжения можно рассматривать как упрошенные модели реальных источников энергии. При определенных условиях, в достаточно узком диапазоне токов и напряжений, внешние характеристики ряда реальных источников энергии могут приближаться к характеристикам идеализированных активных элементов. Так, внешняя характеристика гальванического элемента в области малых токов имеет вид, близкий к внешней характеристике источника напряжения (см. рис. 1.12, б), а внешняя характеристика выходного каскада на транзисторе в определенном диапазоне напряжений приближается к внешней характеристике источника тока (см. рис. 1.14, а).

В то же время свойства реальных источников энергии значительно отличаются от свойств идеализированных активных элементов. Реальные источники энергии обладают конечной мощностью; их внешняя характеристика, как правило, не параллельна оси токов или оси напряжений, а пересекает эти оси в двух характерных точках, соответствующих режимам холостого хода и короткого замыкания (иногда в источниках энергии применяют специальные виды защиты, исключающие работу в предельных режимах или в одном из них).

В реальных источника напряжения ток короткого замыкания имеет конечное значение 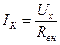, поскольку такие источники характеризуются наличием конечного внутреннего сопротивлений R_вн.

В реальных источниках тока напряжение холостого хода на их зажимах имеет конечное значение U_x=G_вн , поскольку такие источники характеризуются конечным внутренним сопротивлением R_вн=1/G_вн. Поэтому с достаточной для практики точностью внешние характеристики большинства реальных источников энергии могут быть приближенно представлены прямой линией, пересекающей оси токов и напряжений в точках 1 и 2 (рис 1.16 а, б):

U₁=U_x, I₁=0;

U₂=0, I₂=I_к, (1.31)

соответствующий режимам холостого хода и короткого замыкания источника.

Рис. 1.16

Следовательно, реальный источник энергии может быть представлен схемой замещения, состоящей из идеального источника напряжения Е и внутреннего сопротивления R _вн или идеального источника тока I и внутренней проводимости G (рис 1.17, а, б)

Рис 1.17

Полученные схемы замещения реальных источников соответствуют уравнению одной и той же внешней характеристики (рис 1.16 а, б) и, следовательно, их поведение относительно внешних зажимов совершенно одинаково. Выбор той или иной схемы замещения может быть сделан совершенно произвольно, но в ходе расчета цепи может возникнуть необходимость перехода от одной схемы к другой.

Зависимость напряжения на зажимах последовательной схемы замещения от тока определяется уравнением:

, (1.32)

соответствующем внешней характеристике цепи. показанной на рис 1.16, а.

Зависимость между током и напряжением на зажимах параллельной схемы замещения определяется уравнением:

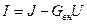, (1.33)

соответствует внешней характеристике цепи, показанной на рис. 1.16,б.

Используя выражения (1.32) – (1.33) можно найти формулы перехода от последовательной схемы замещения к параллельной:

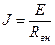; (1.34)

и от параллельной схемы к последовательной:

; (1.35)

Переход от последовательной схемы замещения к параллельной и от параллельной к последовательной возможен только в тех случаях, когда соответственно внутренние сопротивления R_вн или внутренняя проводимость G_вн источника не равны нулю.

Выражения для взаимного преобразования схем замещения источников энергии (1.34) и (1.35) были получены для источников постоянного тока и напряжения. Аналогичные соотношения могут быть наедены и для источников, в которых напряжение и ток являются производными функциями времени.

Лекция составлена доцентом кафедра «Радиоэлектроника»

Руденко Н.В.

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ДГТУ)

Кафедра «Радиоэлектроника»

Руденко Н.В.

ЛЕКЦИЯ № 2

Тема лекции: «ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ»

по дисциплине ОСНОВЫ ТЕОРИИ ЦЕПЕЙ

Ростов-на-Дону

ЛЕКЦИЯ №2

Тема лекции: «ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ»

Учебные вопросы

1. Основные понятия топологии электрических цепей.

2. Понятие о компонентных и топологических уравнениях. Законы Кирхгофа.

3. Основные задачи теории цепей.

Дата добавления: 2013-12-14