Общие сведения. Лекции 18-19. Непрерывная случайная величина

Лекции 18-19. Непрерывная случайная величина

и её характеристики

Непрерывная случайная величина характеризуется тем, что её реализации, в виде численных значений, могут находиться в любой точке интервала: от минимальной до максимальной границы его значений.

Непрерывная случайная величина характеризуется дифференциальной и интегральной функциями распределения вероятностей.

Наиболее широко в практике исследований для обобщения случайных процессов применяется «нормальное распределение плотностей вероятностей». Нормальное распределение (распределение Гаусса).

Дифференциальная функция распределения плотности вероятностей выражается формулой:

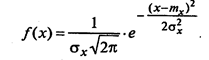
Интегральная функция распределения плотности распределения вероятностей выражается формулой:

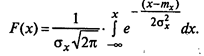
Первичные обобщения реальных процессов, осуществляются посредством использования параметров случайной величины.

В теории вероятностей каждый вид распределения фигурирует как «закон распределения» Формально такой закон закрепляется интегральной и дифференциальной функциями плотности распределения вероятностей.

Среднее значение случайной величины для эмпирических процессов приближённо соответствует теоретическому понятию «математического ожидания М» случайной величины Х, которая характеризуется своими реализациями х_i.

Расчёт математического ожидания для дискретной случайной величины производится по формуле:

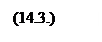
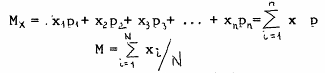
Для непрерывной случайной величины используется формула:

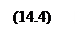
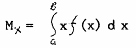
Здесь: М_x - математическое ожидание,

x_i -реализация случайной величины X,

n - число групп с одинаковыми значениями случайной величины,

p_i - относительная частота попадания конкретного значения случайной

величины в соответствующую группу.

Кроме математического ожидания используются, и другие параметры, которые позволяют получить другие полезные сведения о реальном случайном процессе. Параметры случайной величины, с одной стороны, позволяют обобщить ряд её реализаций (из-за большого их количества они становятся необозримы для анализа); с другой стороны, их сопоставление позволяет с определённой степенью уверенности, высказать суждение о случайности (стохастичности) процесса и отнести его к определённому виду (закону) теоретического распределения. Используются также следующие дополнительные параметры.

Мода (M₀). Модой дискретной случайной величины называётся её наиболее вероятное значение, то есть значение, вероятность которого наибольшая. Для непрерывной случайной величины мода - это такое её значение, при котором плотность распределения максимальна.

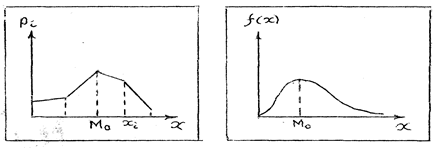
Рис. 14.1. Мода дискретной Рис. 14.2.Мода непрерывной

Дата добавления: 2014-01-05