Параметров распределения

Лекция 20. Оценка эмпирических

Эмпирические ряды распределения, получаемые при обработке первичных статистических данных, оформляются в таблицах или изображаются графически посредством геометрических образов — точек, линий и фигур в различных сочетаниях. Построение эмпирических графиков и диаграмм позволяет установить на первом этапе исследования, к какому типу теоретических распределений ближе полученное эмпирическое распределение. Фактически, любое эмпирическое распределение случайной величины представляет собой некоторую оценку реального процесса в предположении, что он является вероятностным.

Типичной процедурой для обобщения такого рода задач является построение вариационного ряда. Строится он следующим образом.

Весь диапазон значёний «эмпирической» непрерывной случайной величины Х разбивается на интервалы. Далее подсчитывается количество значений m_i случайной величины Х, приходящейся на каждый интервал, и определяется частота ее попадания в данный интервал по формуле:

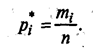
Если случайная величина Х принимает значение, попадающее на границу

i-го и (i + 1)-го интервалов, то это значение учитывается в числе попаданий в (i + 1)-й интервал. Определив, таким образом, частоты попадания случайной величины Х в каждый интервал, получим вариационный (статистический) ряд, который представлен в табл. 14.2.1.

Таблица 14.2.1.

Оптимальная длина интервала определяется по формуле:

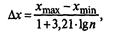
где х _max — х _min это размах вариаций случайной величины Х.

Число интервалов будет равно:

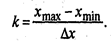
Вариационные ряды могут быть изображены графически в виде полигона частот распределения или гистограммы.

Для построения теоретической кривой распределения исходный статистический ряд распределения аппроксимируется одной из дифференциальных функций f_x теоретического распределения.

При этом выбирается такая функция, которая обеспечивала бы максимальное приближение теоретических данных к эмпирическим.

Для оценки правдоподобия этого приближенного равенства разработано несколько критериев согласия, относительно гипотез выдвинутых относительно

вида эмпирической функции. Наиболее употребительными критериями согласия являются критерий Пирсона и критерий Колмогорова.

Полезность теоретических функций заключается в том, что только они могут обеспечить просто численные расчёты состояний объекта исследования, и, тем более, прогнозные расчёты. Положительное заключение по идентификации эмпирического распределения фактически расценивается как официальное разрешение на пользование всеми инструментами, которыми располагает теория.

В противном случае, использование теоретического аппарата не только бесполезно, но и вредно.

Для того, чтобы пояснить смысл сказанного рассмотрим один пример, где выдвигается гипотеза о том, что эмпирическое распределение плотностей вероятностей, а точнее частостей соответствует закону «нормального распределения.

Воспользуемся примером анализа, приведенном в учебнике В.Е. Гмурмана «Теория вероятностей и математическая статистика» (изд. «Высшая школа» М. 1977г. - с329-332).

Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины — критерия согласия.

Критерием согласия называют критерий проверки гипотезы в предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия: χ² («кси квадрат»), Пирсона, Колмогорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство).

С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Обычно эмпирические и теоретические частоты различаются.

Например:

эмпирические частоты...... 6 13 38 74 106 85 30 10 4

теоретические частоты........3 14 42 82 99 76 37 11 2

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется это либо малым числом наблюдений, либо способом их группировки, либо другими причинами.

Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает, на принятом уроне значимости ее согласие или несогласие с данными наблюдений.

Итак, пусть по выборке объема n получено эмпирическое распределение:

варианты ............ х_i х₁ х₂... х_s

эмп. частоты....... n_i п₁ п₂... п_s

Допустим, что, в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты n_i.

При уровне значимости α требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину χ²:

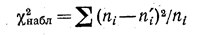
Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретическиё частоты, тем меньше величина критерия (*), и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. делением на п_i достигают уменьшения каждого из слагаемых; в противном случае сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. Разумеется, приведенные соображения не являются обоснованием выбранного критерия, а лишь пояснением.

Доказано, что при п → со закон распределения случайной величины (*) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ² с k тепенями свободы. Поэтому случайная величина (*) обозначена через χ², а сам критерий называют «критерием согласия χ²»

Число степеней свободы находят по равенству k= s—1—r, где s —число групп (частичных интервалов) выборки; r — число параметров предполагаемого распределения, которые оценены по данным выборки.

В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому r=2 и число степеней свободы k = s - 1 - r = s — 1 — 2 = s — З.

Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр λ, поэтому r= 1 и k=s—2. Поскольку односторонний критерий более «жёстко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α:

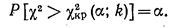
Таким образом, правосторонняя критическая область определяется неравенством:

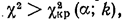
а область принятия нулевой гипотезы — неравенством:

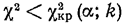
Обозначим значение критерия, вычисленное по данным наблюдений, через χ²_набл и сформулируем правило проверки нулевой гипотезы.

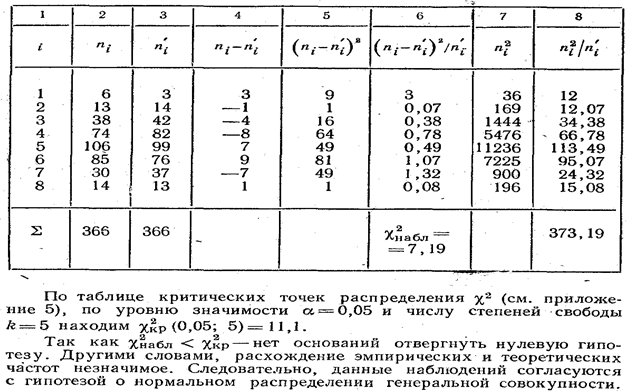
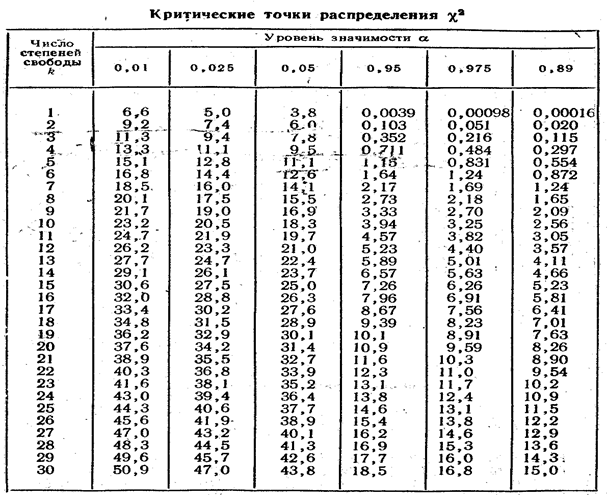
Далее проведём расчёт таблицы критических точек (табл. 14.2.1).
Таблица 14.2.1.

Дата добавления: 2014-01-05