Плотности распределения вероятностей

Плотности распределения вероятностей

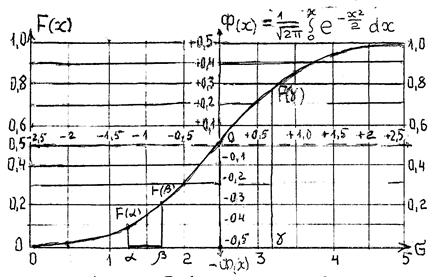
Рис. 14.8. График интегральной функции

По данным графикам распределения можно определить вероятность того, что в очередном испытании измеренное значение случайной величины х_i будет находиться в интервале значений α ≤ х_i ≤ β (при условии, что реальный процесс подчиняется закону нормального распределения).

При использовании дифференциальной функции распределения вероятностей, искомая вероятность будет равна площади криволинейной трапеции (заштрихованная часть графика рис. 14.7).

При использовании интегральной функции: Р(х_i ) = F(β) – F(α) (рис. 14.8).

В организации и проведении статистического эксперимента следует иметь в виду, что его программа всегда ориентирована на выход к некоторым теоретическим функциям распределения, которые закономерно, по мере поступления данных, образуют генеральную совокупность. По этому поводу в математической энциклопедии даётся следующая справка. Генеральная совокупность — понятие теории статистического выборочного метода.

В математической статистике генеральной совокупностью выделяется множество каких-либо однородных элементов, из которого, по определённому правилу, выделяется некоторое подмножество, называемое выборкой.

В простейших случаях контролируемая выборка извлекается из генеральной совокупности случайно (наугад), что с точки зрения теории вероятностей, означает: если генеральная совокупность содержит N элементов и отбирается выборка из n элементов (п < N ), то выбор должен быть осуществлён таким образом, чтобы для любой группы из n элементов вероятность быть извлечённой равнялась n! (N — 1)! N!.

В математической статистике принято результаты однородных наблюдений называть выборкой даже в том случае, когда эти результаты не соответствуют понятию генеральная совокупность, указанному выше.

Понятие бесконечной генеральной совокупности не является логически безупречным и необходимым.

Для решения статистических задач нужна не сама генеральная совокупность, а некоторое, достаточно большое количество однородных данных, которых было бы достаточно, для замены гистограммы на графики функций теории вероятностей соответствующего вида.

С этой целью необходимо знать закон распределения генеральной совокупности.

Если закон распределения неизвестен, то имеются основания предположить, что он имеет определенный вид (назовем его А), поэтому выдвигают гипотезу: генеральная совокупность распределена по закону А.

Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны.

Если есть основания предположить, что неизвестный параметр θ равен определенному значению θ₀, тогда выдвигают гипотезу: θ=θ_0.

Таким образом, в этой гипотезе речь идет о предполагаемой величине параметре одного известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или, нескольких распределений, о независимости выборок и многие другие.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Например, статистическими являются гипотезы:

1) генеральная совокупность распределена по закону Пуассона;

2) дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, и во второй — о параметрах двух известных распределений.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу.

Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.

По этой причине эти гипотезы целесообразно различать.

Нулевой (основной) называют выдвинутую гипотезу Н₀, а альтернативной гипотезой называют противоречащую ей, конкурирующую гипотезу.

В практике работы с случайными величинами большое значение придают мере их рассеяния,

то есть отклонения их от средних значений, а также экстремальным значениям.

Дата добавления: 2014-01-05