
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Постановка задачи параметрической оптимизации
|
|
|
|
Основы оптимизации и методы синтеза систем управления
Пусть поведение одномерной системы управления описывается дифференциальным уравнением вида:
| D(p) y(t) = C(p) r(t), p = d / dt | (3.1) |
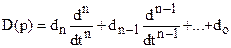 .
.
D(p) – операторная функция преобразования. Аналогично можно записать операторную функцию C(p). Особого внимания заслуживает рассмотрение преобразования входного сигнала r(t) в выходной y (t):
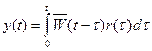
| (3.2) |
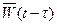 – ядро операторного преобразования. Если в системе управления выделить вектор варьируемых параметров х, то последняя формула примет вид:
– ядро операторного преобразования. Если в системе управления выделить вектор варьируемых параметров х, то последняя формула примет вид:
y(t,x) = 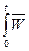 (x, t-t) r(t) dt (x, t-t) r(t) dt
| (3.3) |
Пусть на качество САУ наложены ограничения вида:
| y (x, 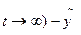 | £ | £ 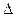
| (3.4) |
| h (x, t > Tрег) - h (х, t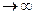 )| £ )| £ 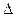
| (3.5) |
| h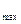 (x, t) - h (х, t (x, t) - h (х, t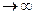 )| £ )| £ 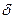 , ,  t Î (0,Tрег) t Î (0,Tрег)
| (3.6) |
Здесь приняты следующие обозначения: - 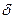 - абсолютное значение величины перерегулирования;
- абсолютное значение величины перерегулирования; 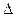 - статическая ошибка; h (x,t) - переходная характеристика; h (х, t
- статическая ошибка; h (x,t) - переходная характеристика; h (х, t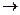 ¥) - установившееся значение переходного процесса;
¥) - установившееся значение переходного процесса; 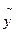 - требуемое значение выходной (управляемой) переменной. Если от одномерной системы управления перейти к многомерной, и в качестве х рассматривать вектор варьируемых параметров, то любая компонента i вектора управляемых параметров может быть представлена формулой:
- требуемое значение выходной (управляемой) переменной. Если от одномерной системы управления перейти к многомерной, и в качестве х рассматривать вектор варьируемых параметров, то любая компонента i вектора управляемых параметров может быть представлена формулой:
yi (x, t) = 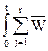 ij (x, t - t) rj(t) dt ij (x, t - t) rj(t) dt
| (3.7) |
Задача параметрической оптимизации для многомерной САУ, поведение которой описывается системой уравнений (3.7), состоит в определении таких значений вектора x, принадлежащих заданной области, при которых САУ будет обладать заданными характеристиками. Решение задачи сложный и трудоемкий процесс, часто с трудно разрешимыми ситуациями. «Метод проб и ошибок» в поиске рациональных параметров не является эффективным. Рассмотрим решение на основе моделирования процессов в комплексной плоскости. В качестве модели САУ будем рассматривать модель вида:
Y(x, s) = W(x,s) * R(s), 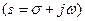
| (3.8) |
Без рассмотрения подробностей воспользуемся доказанным утверждением. Для выполнения условий (3.4) - (3.6), налагаемых на качество системы управления во временной области, достаточно выполнение следующих условий в комплексной плоскости:
| s Y(x,s) - 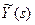 | |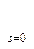 £ £ 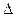
| (3.9) |
| s Î W | (3.10) |
В связи с этим задача параметрической оптимизации может быть сформулирована следующим образом. Для многомерной системы управления, поведение которой описывается системой уравнений (3.8) требуется найти такое значение вектора оптимизируемых параметров х= хопт. (х - вектор неизвестных коэффициентов передаточных функций управляющей части), при котором система управления будет обладать требуемым качесвом (3.9) – (3.10) за счет максимального приближения к эталонной системе управления, чтобы целевая функция F(x), характеризующая такое приближение, принимала минимальное значение
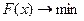 .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 536; Нарушение авторских прав?; Мы поможем в написании вашей работы!