
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методика решения задачи параметрической оптимизации
|
|
|
|
Прежде чем перейти к решению задачи, рассмотрим влияние полюсов и нулей на статические и динамические характеристики системы управления.
Запишем выражение установившегося процесса на выходе объекта управления:
Y(x, s) = W(x,s) *R(s), (s = 0).
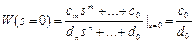
Отметим, что если нуль и полюс находятся близко друг от друга, а именно: на расстоянии менее чем 0.1 модуля, то влияние такого полюса ослабляется нулем, то есть полюс не оказывает существенного влияния на динамические характеристики системы управления. Рассмотрим пример. Пусть выходная функция Y(s) имеет вид:
 , (s1п = - 5.2, s2п = - 8, s1н = -5).
, (s1п = - 5.2, s2п = - 8, s1н = -5).
Поскольку расстояние между нулем и первым полюсом намного меньше модуля корня, то влиянием ближайшего к нулю полюса можно пренебречь, так как он оказывает несущественное влияние на динамику системы управления в целом. Пусть многомерная система управления, описываемая системой уравнений (3.8), не удовлетворяет требованиям качества, это означает, что некоторые полюсы выходят за границу области W или нули оказывают отрицательное влияние на качество управления. Идеальной системой управления будем считать такую, которая имеет заданное расположение полюсов и нулей или заданный корневой годограф. Для решения задачи параметрической оптимизации введем в рассмотрение расположение идеальных полюсов и нулей. Воспользовавшись известными формулами перехода от корней алгебраического уравнения к его коэффициентам можно записать:

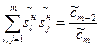 …
… 
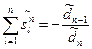
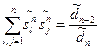 …
… 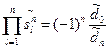
Эти соотношения позволяют найти обобщенные передаточные функции каналов входы - выход эталоной системы уравления вида:
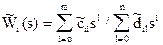 , (i = 1,…,y), , (i = 1,…,y),
| (3.11) |
где y - число выходов системы управления. Обобщенные передаточные функци каналов оптимизируемой по параметрам системы управления представим в виде:
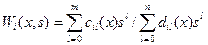
| (3.12) |
Таким образом, имеем эталоные обобщенные передаточные функции каналов входы - выход в виде (3.11) и реальные в виде (3.12). Метод параметрической оптимизации основан на приближении реальной системы управления к эталоной как можно ближе за счет оптимальной настройки параметров x. Введем в рассмотрение оптимизируемую функцию как средне - квадратичную ошибку аппроксимации по коэффициентам передаточных функций эталоной и оптимизируемой по параметрам систем управления. Целевая функция примет вид:
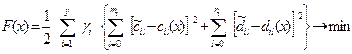
Здесь приняты следующие обозначения: cil(x), 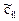 - соответственно коэффициенты полиномов Сi(x,s) и
- соответственно коэффициенты полиномов Сi(x,s) и 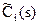 ; dil(x),
; dil(x), 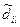 - соответственно коэффициенты полиномов Di(x,s) и
- соответственно коэффициенты полиномов Di(x,s) и 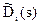 ; gi - весовые коэффициенты, назначение которых разделять каналы управления по степени значимости.
; gi - весовые коэффициенты, назначение которых разделять каналы управления по степени значимости.
Функция F(x) – алгебраическая. Для нахождения ее минимума на множестве X, заданном ограничениями вида: jl(х) = 0, (l=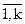 ), воспользуемся подходом основанным на введении неопределенных множителей Лагранжа
), воспользуемся подходом основанным на введении неопределенных множителей Лагранжа 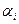 , что предполагает решение системы уравнений вида:
, что предполагает решение системы уравнений вида:
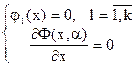 Ф(x,a) = F(x)+ Ф(x,a) = F(x)+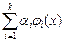
| (3.13) |
где k - размерность вектора х. Первые уравнения вытекают из приравнивания к нулю производных функции Ф(x, a) по переменным вектора a. Минимум функций F(x) и Ф(x, a) будет достигнут в точке x = xопт, найденной из решения (3.13), если в этой точке будет выполнено условие положительности квадратичной формы:
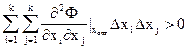
| (3.14) |
где 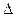 xi,
xi, 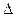 xj - малые приращения компонент вектора х. Следовательно, чтобы x = xопт была точкой, в которой целевая функция принимает минимальное значение, необходимо и достаточно, чтобы в этой точке выполнялись условия (3.13) и (3.14). Для решения (3.13) используются изветные методы, в частности, численный метод решения системы нелинейных алгебраических уравнений Ньютона - Рафсона. Отметим, что любые неравенства, накладываемые на неизвестные параматры вектора х, можно привести к равенствам, вводя дополнительные неизвестные. Например, пусть имеем ограничение вида: х
xj - малые приращения компонент вектора х. Следовательно, чтобы x = xопт была точкой, в которой целевая функция принимает минимальное значение, необходимо и достаточно, чтобы в этой точке выполнялись условия (3.13) и (3.14). Для решения (3.13) используются изветные методы, в частности, численный метод решения системы нелинейных алгебраических уравнений Ньютона - Рафсона. Отметим, что любые неравенства, накладываемые на неизвестные параматры вектора х, можно привести к равенствам, вводя дополнительные неизвестные. Например, пусть имеем ограничение вида: х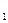 <5, которое можно переписать в виде: х
<5, которое можно переписать в виде: х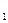 =5 - х
=5 - х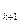 , где х
, где х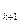 дополнительно вводимый параметр, подлежащий определению наравне с остальными параметрами вектора х. Рассмотрим применение методики параметрической оптимизации на конкретной задаче.
дополнительно вводимый параметр, подлежащий определению наравне с остальными параметрами вектора х. Рассмотрим применение методики параметрической оптимизации на конкретной задаче.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 465; Нарушение авторских прав?; Мы поможем в написании вашей работы!