Виды геометрических характеристик

Рассмотрим произвольное плоское сечение площадью А в системе отсчёта YX (рис. 4.2).

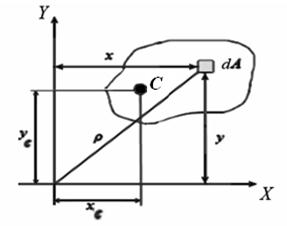
Рис.4.2

Любая из геометрических характеристик сечения может быть представлена в виде интегральной функци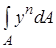и или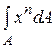. При n = 0 получается площадь сечения 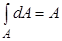. При n = 1 имеем с татический момент площади относительно оси X или Y

(4.1)

Интегрируя, можно убедиться, что статический момент площади относительно оси равен произведению площади на расстояние от центра тяжести сечения с до рассматриваемой оси:

(4.2)

здесь 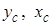− координаты центра тяжести сечения. Из выражений (4.2) следует, что статический момент сечения относительно оси, проходящей через центр тяжести, равен нулю.

Эта характеристика помогает определить положение центра тяжести сложного составного сечения.

Размерность статического момента − см ³ или м ³; он может быть как положительным, так и отрицательным.

При n = 2 интегралы произведения элемента площади dA на квадрат расстояния его до осей представляют осевые моменты инерции

. (4.3)

Размерность осевых моментов инерции − см⁴, м⁴; они всегда положительны.

Если под интегралом произведение элемента площади на квадрат расстояния его до точки О (полюса), получается характеристика, называемая полярным моментом инерции

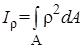. (4.4)

Подставляя в (4.4) 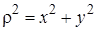, получаем связь между осевыми и полярным моментом инерции сечения:

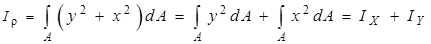. (4.5)

Интегральная функция вида 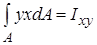позволяет оценить ещё одну геометрическую характеристику центробежный момент инерции сечения. Центробежный момент инерции может быть положительным, отрицательным и даже равным нулю. Оси, относительно которых центробежный момент инерции сечения равен нулю, называют главными. Осевые моменты инерции относительно главных осей достигают экстремальных значений.

Дата добавления: 2014-01-05