Система аксиом Вейля

Т.М. Соромотина

Систему аксиом Вейля (или векторную аксиоматику) построил Герман Вейль (1885–1955) – немецкий математик и физик. Его труды относятся к различным областям математики (математический анализ, алгебра, геометрии, философия математики).

Общая схема аксиоматического построения геометрии:

1) Перечисляются основные (неопределяемые) понятия и отношения;

2) формулируются аксиомы – предложения, в которых указываются свойства основных понятий;

3) вводятся новые понятия, которые определяются через основные (или ранее введенные);

4) вводятся новые теоремы – предложения, которые доказываются с помощью аксиом (или ранее доказанных теорем);

Этой схеме будем следовать при изложении геометрии, изучая теоремы, с которыми мы хорошо знакомы из школьного курса геометрии. Необычными будут определения фигур и доказательства теорем. Все доказательства проводятся на основе свойств векторов, сформулированных в аксиомах.

Векторная аксиоматика предполагает, что задана некоторая числовая система, для построения евклидовой геометрии будем рассматривать множество R действительных чисел со всеми его свойствами.

В качестве основных понятий системы аксиом Вейля считаются следующие: точка, вектор, сложение векторов, умножение вектора на число, скалярное умножение, отношение принадлежности, связывающее точки с векторами.

Введем обозначения: А, В, С, … – точки; , , 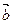, , 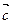, 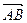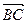… – векторы; Е – множество точек; V – множество векторов; R – множество действительных чисел. Основные отношения обозначим f ₁, f ₂, f ₃, f ₄:

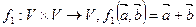
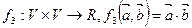
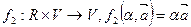
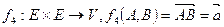
Отношение f ₁ каждым двум векторам 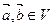ставит в соответствие вектор 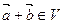, называемый суммой векторов и 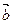. Отношение f ₂ каждому вектору 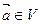и числу 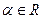ставит в соответствие вектор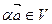, называемый произведением вектора на число a. Отношение f ₃ каждым двум векторам 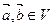ставит в соответствие число 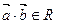, называемое скалярным произведением векторов и 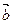. Отношение f ₄ каждым двум точкам 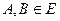ставит в соответствие вектор 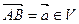. В этом случае точку А называют началом вектора 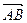, а точку В – концом вектора .

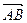Сформулируем аксиомы, разбив их на четыре группы: аксиомы линейного векторного пространства, аксиомы размерности, аксиомы скалярного умножения (метрическая), аксиомы связи точек и векторов.

I. Аксиомы линейного векторного пространства.

Для любых векторов 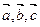и любых действительных чисел a, b справедливы следующие утверждения:

V ₁. 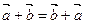. V ₅. .

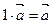V ₂. 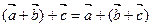. V ₆. .

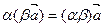V ₃. $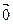/ 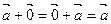. V ₇. .

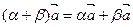V ₄. $–/ 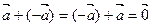. V ₈. .

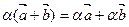Множество V векторов, для которых определено сложение, умножение на действительное число, удовлетворяющее аксиомам V₁–V₈ называют векторным пространством.

II. Аксиомы размерности.

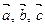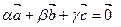D ₁. Существуют такие три вектора , что Û .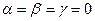

D ₂. Для любых четырех векторов 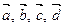существуют такие числа a, b, g, d, что выполняется равенство 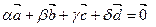, причем числа a, b, g, d одновременно не равны 0, т.е. (a, b, g, d)¹(0,0,0,0).

III. Аксиомы скалярного умножения.

Для любых векторов 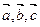и любого действительного числа a справедливы следующие утверждения:

Е ₁. 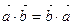. Е ₃. .

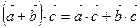Е ₂. 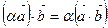. Е ₄. 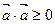, причем 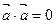Û.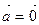

Векторное пространство V, в котором определено скалярное произведение двух векторов, удовлетворяющее аксиомам Е ₁– Е ₄, называют евклидовым векторным пространством.

IV. Аксиомы связи точек и векторов.

Т ₁. Существует хотя бы одна точка, т.е. Е ¹Æ.

Т ₂. Аксиома откладывания вектора от точки. Для любой точки А и любого вектора 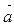существует единственная точка В такая, что .

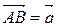Т 3. Аксиома треугольника. Для любых точек А, В, С выполняется равенство .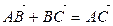

Сформулировали систему аксиом Вейля: 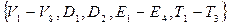. Аксиомы первой группы определяют V как линейное векторное пространство. Аксиомы размерности утверждают, что V – трехмерное векторное пространство, в котором существует хотя бы один базис, состоящий из трех линейно независимых векторов. Аксиомы первых трех групп определяют множество V как трехмерное евклидово линейное векторное пространство.

Учитывая аксиомы, для множества векторов введем обозначение V ³, где индекс означает размерность пространства. Множество Е ³ назовем трехмерным евклидовым пространством, а пространство V ³ – пространством переносов для Е ³. Систему аксиом можно дать в компактной форме, если аксиомы I, II, III групп заменить одной аксиомой:

А. Множество является действительным трехмерным евклидовым линейным векторным пространством.

Тогда система аксиом будет состоять из четырех аксиом: .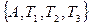

Дата добавления: 2014-01-05