Отрезок. Луч. Полуплоскость. Полупространство

Определение 4.

Отрезком АВ называется множество точек, состоящее из точек А, В (концов отрезка) и всех точек, лежащих между ними (внутренних точек отрезка) или в математических символах .

Обозначается: [ АВ ].

Определение 5.

Лучом с началом М ₀ и направляющим вектором называется множество всех точек, удовлетворяющее условию: 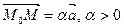или .

Обозначается: луч или .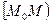

При a >0 луч называют открытым, при a ³0 – замкнутым.

Свойства луча:

1. Луч (открытый или замкнутый) является частью прямой (докажите самостоятельно).

2. В качестве направляющего вектора луча можно взять любой вектор (a >0) (докажите самостоятельно).

3. Если точки А и В принадлежат лучу , то начало луча М ₀ не лежит между точками А и В.

Доказательство. Из определения 5 следует, что , 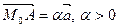(рис. 4.8).

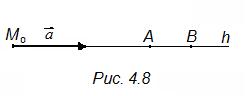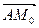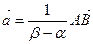Выразим вектор через , выразив предварительно оба через . По аксиоме Т₃ , откуда и 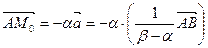. Если a < b, то 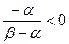. Если a > b, то . Это означает, что точка М ₀ не лежит между точками А и В.

Теорема 10.

Любая точка прямой разбивает прямую на два и только два луча, причем точка лежит между любыми двумя точками, принадлежащими разным лучам, и не лежит между точками, принадлежащими одному лучу.

Доказательство. Пусть s – прямая, А Î s, 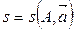(рис. 4.9). Лучи , лежат на одной прямой.

Любой луч , где , будет лучом этой прямой. Если a >0, то h=s ₁; если a <0, то где – a >0 и h=s ₂.

Пусть В Î s ₁ и С Î s ₂, тогда 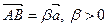, и . Выразим вектор через 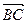. По аксиоме Т₃ 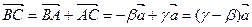; , т.е. . Так как 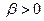, , 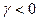то 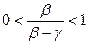. Значит, что А / ВС, т.е. если точки В и С принадлежат разным лучам s ₁ и s ₂ соответственно, то точка А лежит между В и С.

Если точки В и С принадлежат только одному из лучей s ₁ и s ₂, то точка А не лежит между В и С (по свойству 3). Теорема доказана.

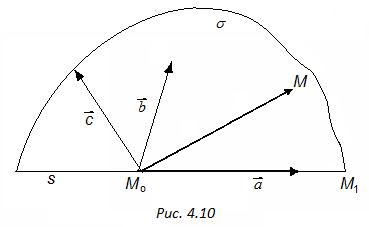
Определение 6.

Полуплоскостью с границей называется множество точек 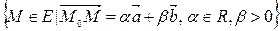(рис. 4.10).

Свойства полуплоскости:

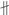
1. Полуплоскость , , 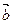является частью плоскости (докажите самостоятельно).

2. Элементы, определяющие полуплоскость, можно заменять на другие. Границей полуплоскости является прямая s, по свойствам которой начальную точку М ₀ можно заменить на М ₁Î s, а направляющий вектор – на любой вектор 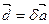. Вектор 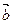по свойствам плоскости можно заменить на любой вектор 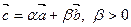. Докажите, что полуплоскость совпадает с полуплоскостью .

Теорема 11.

Любая прямая, лежащая на плоскости, разбивает плоскость на две полуплоскости. Если точки P и Q лежит между в разных полуплоскостях, то отрезок PQ пересекает прямую, если точки лежат в одной полуплоскости, то отрезок PQ не пересекает прямую.

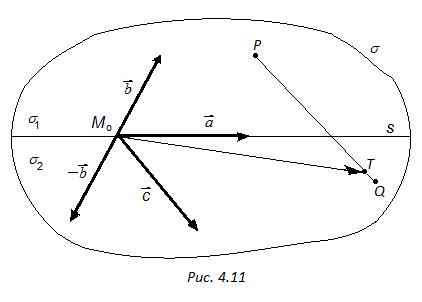
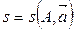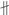
Доказательство. Пусть прямая лежит в плоскости s (рис. 4.11). Тогда плоскость можно задать так: , 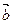. Рассмотрим две полуплоскости и ; .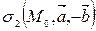

Пусть 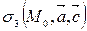– произвольная полуплоскость плоскости s с границей s, тогда 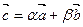. Если b >0, то , если b <0, то 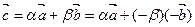, – b >0 и 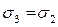(по свойству 2).

Пусть P и Q – точки плоскости s, не лежащие на прямой s. Тогда и 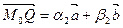(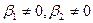). Рассмотрим точку Т отрезка PQ, тогда . Выразим вектор через базисные векторы и :

,

.

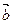Обозначим коэффициент при векторе 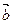и исследуем его значение в зависимости от положения точки Т. Если Т=Р, то r =0, , если Т=Q, то r =1, .

Если точки P и Q лежат в разных полуплоскостях, то числа b ₁ и b ₂ имеют разные знаки. Функция f (р) непрерывна и принимает на концах промежутка [0; 1] разные знаки, следовательно существует 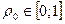, для которого 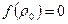. Точка Т, соответствующая этому значению, является точкой пересечения прямой s и отрезка PQ. Если точки P и Q лежат в одной полуплоскости, то b ₁ и b ₂ имеют один и тот же знак, этот же знак имеют все числа f (р) при , , а отрезок PQ не пересекает прямую.

Теорема доказана.

Задание. По аналогии с определением и свойствами полуплоскости сформулируйте определение и свойства полупространства. Докажите эти свойства.

Дата добавления: 2014-01-05