
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плоскость. В школьном курсе геометрии прямая рассматривается как основное (неопределяемое) понятие
|
|
|
|
Прямая
В школьном курсе геометрии прямая рассматривается как основное (неопределяемое) понятие. Поскольку в данной аксиоматике основные понятия – точка и вектор, то прямую необходимо определить через них.
Определение 1.
Прямой 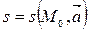 с начальной точкой М0 и направляющим вектором
с начальной точкой М0 и направляющим вектором 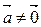 называется множество всех точек М пространства Е, удовлетворяющих условию
называется множество всех точек М пространства Е, удовлетворяющих условию  , где aÎR.
, где aÎR.
На языке математических символов это определение можно записать так: 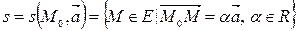 . Можно изменить определение, учитывая, что множество векторов
. Можно изменить определение, учитывая, что множество векторов 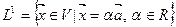 является одномерным линейным векторным пространством и называется направляющим подпространством прямой. Тогда
является одномерным линейным векторным пространством и называется направляющим подпространством прямой. Тогда 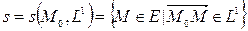 .
.
Теорема 1.
Прямые существуют. Каждая прямая содержит бесконечно много точек. Существует хотя бы одна точка, не лежащая на данной прямой.
Доказательство. По аксиоме Т1 существует хотя бы одна точка М 0Î Е. Так как пространство V трехмерно, то существует хотя бы один вектор 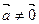 . Рассмотрим все векторы
. Рассмотрим все векторы  . По аксиоме Т2 существуют точки М Î Е и удовлетворяющие условию
. По аксиоме Т2 существуют точки М Î Е и удовлетворяющие условию  . Множество всех таких точек М есть прямая (по определению 1).
. Множество всех таких точек М есть прямая (по определению 1).
Так как R – бесконечное множество, то на прямой существует бесконечное множество точек. Так как пространство трехмерно, то существует хотя бы один вектор 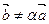 . По аксиоме Т2 существует точка N такая, что
. По аксиоме Т2 существует точка N такая, что  (рис. 4.1). Теорема доказана.
(рис. 4.1). Теорема доказана.

Теорема 2. О замене начальной точки и направляющего вектора
Для любой прямой 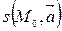 в качестве начальной точки можно выбрать любую точку, лежащую на прямой, а в качестве начального вектора – любой вектор
в качестве начальной точки можно выбрать любую точку, лежащую на прямой, а в качестве начального вектора – любой вектор  .
.
Дано: 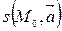 ,
, 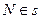
 .
.
Доказать: 1) 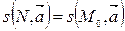 ; 2)
; 2)  .
.
Доказательство. Множества совпадают, если каждое из них является подмножеством другого.
1) Пусть М Î s, тогда  . N Î s, тогда
. N Î s, тогда 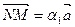 . По аксиоме Т3
. По аксиоме Т3  , т.е.
, т.е.  , где
, где  . Доказали, что если М Î s, то
. Доказали, что если М Î s, то  , а так как М – произвольная точка прямой s, то
, а так как М – произвольная точка прямой s, то 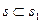 .
.
Пусть  , тогда
, тогда  . По аксиоме Т3
. По аксиоме Т3 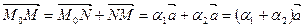 , т.е. М Î s и
, т.е. М Î s и 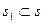 .
.
Так как 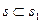 и
и 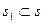 , то
, то  .
.
2) Пусть М Î s, тогда  . Так как по условию
. Так как по условию  (откуда
(откуда 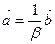 ), то
), то 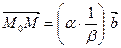 , т.е.
, т.е. 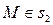 и
и 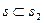 .
.
Пусть 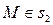 , тогда
, тогда 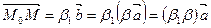 , т.е. М Î s и
, т.е. М Î s и 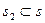 .
.
Так как 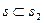 и
и 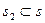 , то
, то 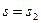 .
.
Теорема доказана.
Теорема 3.
Через любые две различные точки проходит единственная прямая.
Дано: 
Доказать: 1) существует прямая s:  ;
;
2) прямая s – единственная.
Доказательство.
1) Существование. Для доказательства достаточно указать начальную точку прямой и ее направляющий вектор. В качестве начальной точки можно выбрать любую из данных точек, например М 1. В качестве направляющего вектора выберем 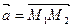 (рис. 4.2), по условию
(рис. 4.2), по условию 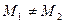 , значит,
, значит, 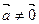 (по следствию С1).
(по следствию С1).
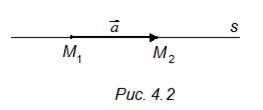 Рассмотрим прямую
Рассмотрим прямую  и докажем, что прямая проходит через данные точки. По определению прямой
и докажем, что прямая проходит через данные точки. По определению прямой 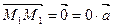 , следовательно,
, следовательно,  .
.  , следовательно,
, следовательно,  .
.
Существование прямой, проходящей через две различные точки доказано.
Замечание. Прямую  можно обозначать так:
можно обозначать так: 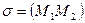 .
.
2) Единственность. Пусть прямая 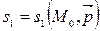 также проходит через данные точки М 1 и М 2. По теореме 2 заменим начальную точку
также проходит через данные точки М 1 и М 2. По теореме 2 заменим начальную точку 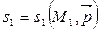 . Так как
. Так как  , то
, то 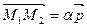 , т.е.
, т.е.  . Доказали, что
. Доказали, что 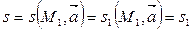 . По теореме 2 заменим направляющий вектор
. По теореме 2 заменим направляющий вектор 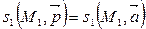 . Прямая, проходящая через две данные точки единственна.
. Прямая, проходящая через две данные точки единственна.
Теорема доказана.
Замечание. Любой ненулевой вектор в направляющем подпространстве образует в нем базис, поэтому допускаем для направляющего вектора прямой  название базисный вектор
название базисный вектор 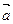 прямой s или, коротко, базис.
прямой s или, коротко, базис.
Плоскость задается начальной точкой и базисом, состоящим из двух неколлинеарных векторов.
Определение 2.
Плоскостью  с начальной точкой М 0 и направляющими векторами
с начальной точкой М 0 и направляющими векторами 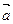 и
и 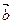 ,
, 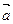
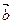 , называется множество точек М пространства, удовлетворяющих условию
, называется множество точек М пространства, удовлетворяющих условию 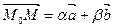 , где a,b ÎR, т.е.
, где a,b ÎR, т.е.
 .
.
 Направляющим подпространством плоскости s является двумерное векторное пространство
Направляющим подпространством плоскости s является двумерное векторное пространство

с базисом  . Определение плоскости можно записать так:
. Определение плоскости можно записать так:
 .
.
Далее доказываются теоремы о свойствах плоскостей, во многом аналогичные теоремам о свойствах прямых. Условимся считать, что теоремы, доказательства которых не приводятся, рассматриваются в качестве упражнений.
Теорема 4.
В пространстве существует хотя бы одна плоскость. Каждая плоскость содержит бесконечно много точек. Существует хотя бы одна точка, не лежащая на данной плоскости.
Доказательство. По аксиоме Т1 существует хотя бы одна точка М 0Î Е. Так как пространство V трехмерно, то существует хотя бы одна пара линейно независимых (неколлинеарных) векторов  .
.
Откладывая от точки М 0 векторы  (аксиома Т2), будем получать множество точек М, которое и будет плоскостью
(аксиома Т2), будем получать множество точек М, которое и будет плоскостью  . Так как R бесконечно, то на плоскости существует бесконечно много точек.
. Так как R бесконечно, то на плоскости существует бесконечно много точек.
Рассмотрим точку Р такую, что 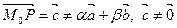 , тогда Р Ï s. Такой вектор всегда существует (объясните, почему?). Теорема доказана.
, тогда Р Ï s. Такой вектор всегда существует (объясните, почему?). Теорема доказана.
Теорема 5. О замене начальной точки и направляющих векторов
Для любой плоскости  в качестве начальной точки можно выбрать любую точку, лежащую на этой плоскости, а в качестве направляющих векторов – любые векторы
в качестве начальной точки можно выбрать любую точку, лежащую на этой плоскости, а в качестве направляющих векторов – любые векторы 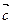 и
и  , удовлетворяющие условию:
, удовлетворяющие условию:
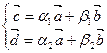 , где
, где  и
и  .
.
Дано:  , N Î s,
, N Î s, 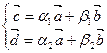 , где
, где  и
и  .
.
Доказать: 1)  =
=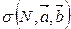 ; 2)
; 2)  =
= .
.
Доказательство. 1) Обозначим  и
и 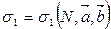 Множества совпадают, если каждое из них является подмножеством другого.
Множества совпадают, если каждое из них является подмножеством другого.
Пусть М – произвольная точка плоскости s, М Î s, тогда по определению плоскости  . По аксиоме Т3
. По аксиоме Т3  . Так как N Î s, то
. Так как N Î s, то 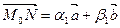 и
и 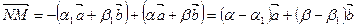 . Отсюда следует, что
. Отсюда следует, что  .
.
Пусть М Î s 1, тогда  ,
,  = =
= = . Следовательно, что
. Следовательно, что 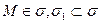 .
.
Таким образом, 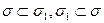 , значит,
, значит, 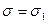 .
.
2) Обозначим  и
и  . Пусть М Î s 2, тогда
. Пусть М Î s 2, тогда 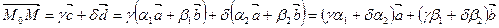 , следовательно,
, следовательно,  .
.
Пусть М Î s, тогда  . По условию
. По условию  , значит, векторы
, значит, векторы 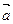 и
и 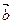 однозначно выражаются через векторы
однозначно выражаются через векторы 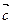 и
и  (система уравнений имеет единственное решение):
(система уравнений имеет единственное решение): 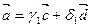 ,
,  (выполните вычисления самостоятельно и найдите значения
(выполните вычисления самостоятельно и найдите значения  ). Следовательно,
). Следовательно, 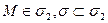 .
.
Таким образом, 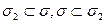 , значит,
, значит, 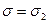 . Теорема доказана.
. Теорема доказана.
Рассмотрим теоремы о способах задания плоскости (теоремы 6-8).
Теорема 6.
Через любые три точки, не лежащие на одной прямой, проходит плоскость и только одна.
Дано: А, В, С – неколлинеарные точки.
Доказать: 1) существует плоскость s: А Î s, В Î s, С Î s; 2) плоскость s – единственная.
Доказательство.
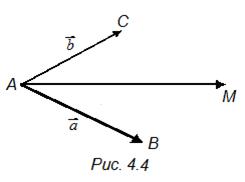
1) В качестве начальной точки можно взять любую из данных точек, например точку А. В качестве базиса выберем векторы 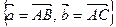 ,
, 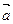
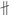
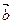 , так как точки А, В, С не лежат на одной прямой (рис. 4.4).
, так как точки А, В, С не лежат на одной прямой (рис. 4.4).
 Докажем, что плоскость
Докажем, что плоскость 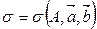 проходит через данные точки:
проходит через данные точки:
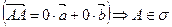 ,
,
 ,
,
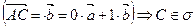 .
.
Таким образом, плоскость, проходящая через неколлинеарные точки А, В, С существует.
Замечание. Плоскость 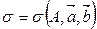 можно обозначить так:
можно обозначить так: 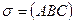 .
.
2) Докажем, что плоскость единственна. Допустим, что существует плоскость 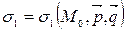 , проходящая через точки А, В, С, т.е. А Î s 1, В Î s 1, С Î s 1. По теореме 5 в качестве начальной точки выберем точку А, т.е.
, проходящая через точки А, В, С, т.е. А Î s 1, В Î s 1, С Î s 1. По теореме 5 в качестве начальной точки выберем точку А, т.е. 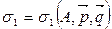 . Так как В Î s 1, то
. Так как В Î s 1, то 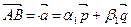 ; так как С Î s 1, то
; так как С Î s 1, то 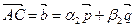 , причем
, причем 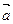
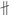
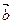 , так как А, В, С не коллинеарны. Тогда по теореме 5 плоскость базис
, так как А, В, С не коллинеарны. Тогда по теореме 5 плоскость базис  можно заменить на
можно заменить на  , т.е.
, т.е.  .
.
Таким образом, плоскость, проходящая через неколлинеарные точки А, В, С единственна. Теорема доказана.
Теорема 7.
Через любые две пересекающиеся прямые проходит плоскость и только одна.
Теорема 8.
Через любые точку и не проходящую через нее прямую проходит плоскость и только одна.
Теоремы 7 и 8 докажите самостоятельно.
Теорема 9.
Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.
Дано: s – прямая, А Î s, В Î s; s – плоскость, А Î s, В Î s.
Доказать: s Ì s.
Доказательство. Прямую s зададим начальной точкой А и направляющим вектором 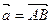 :
: 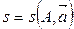 . По теореме 5 плоскость зададим так:
. По теореме 5 плоскость зададим так: 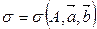 ,
, 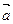
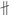
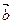 (рис. 4.5).
(рис. 4.5).
 Пусть точка М Î s, тогда по определению прямой
Пусть точка М Î s, тогда по определению прямой 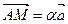 . По определению плоскости s вектор
. По определению плоскости s вектор 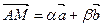 , следовательно, М Î s. Так как точка М – произвольная точка прямой s, то s Ì s.
, следовательно, М Î s. Так как точка М – произвольная точка прямой s, то s Ì s.
Теорема доказана.
Дальнейшее построение геометрии на плоскости требует введения таких фигур, как отрезок, луч, полуплоскость, которые определяются через отношение «лежать между» для точек и дают возможность определить другие фигуры: углы, треугольники, многоугольники и т.д.
3. Отношение «лежать между»
Определение 3.
Точка В лежит между точками А и С, если 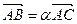 , 0< a <1.
, 0< a <1.
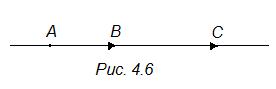
Обозначение: В / АС (рис. 4.6).
Из определения следует: 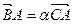 ,
,
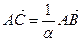 .
.
Свойства отношения «лежать между»:
1. Если В / АС, то А, В, С – три различные точки одной прямой.
2. Если В / АС, то В / СА.
3. Из трех точек прямой одна и только одна лежит между двумя другими.
Докажем свойства, имея в виду, что
1. Пусть В / АС, тогда 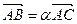 (0< a <1). Рассмотрим прямую
(0< a <1). Рассмотрим прямую 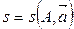 ,
, 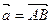 , следовательно, А Î s, В Î s, С Î s.
, следовательно, А Î s, В Î s, С Î s.
2. По аксиоме Т3 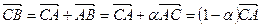 , т.е.
, т.е.  . Так как 0< a <1, то 0<1– a <1, т.е. В / СА.
. Так как 0< a <1, то 0<1– a <1, т.е. В / СА.
3. Пусть А, В, С – точки, лежащие на одной прямой  , причем
, причем 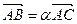 . Рассмотрим расположение точек в зависимости от значения a.
. Рассмотрим расположение точек в зависимости от значения a.
1) Пусть 0< a <1, тогда В / АС по определению (рис. 7 а).
2) Пусть a >1. Выразим вектор 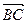 через
через  (или
(или 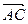 через
через 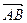 ). По аксиоме Т3 и определению 3
). По аксиоме Т3 и определению 3  , откуда
, откуда  .
.
Так как a >1, то 0< <1 и 0<
<1 и 0<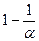 <1. Значит, С / АВ (рис. 7 б).
<1. Значит, С / АВ (рис. 7 б).
3) Пусть a <0. Выразим векторы  через
через 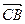 (или
(или  через
через 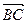 ). По аксиоме Т3
). По аксиоме Т3  , откуда
, откуда  ,
, 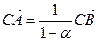 .
.
Так как a <0, то 1– a >1 и 0<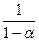 <1. Следовательно, А / ВС (рис. 7 в).
<1. Следовательно, А / ВС (рис. 7 в).

|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1788; Нарушение авторских прав?; Мы поможем в написании вашей работы!