Проверка требования непротиворечивости

Требования к системе аксиом Вейля

Для того чтобы система аксиом могла использоваться в качестве основания теории, к ней предъявляются определенные требования. Рассмотрим основные: непротиворечивости (совместности), независимости, полноты.

Определение 1

Система аксиом называется непротиворечивой или совместной, если из нее нельзя вывести двух следствий, из которых одна отрицает другую.

Определение означает, что совокупность следствий (теорем), которая строится на данной системе аксиом, не содержит противоречивой теории. Способ проверки системы аксиом на непротиворечивость – построение ее модели в некоторой непротиворечивой теории.

Определение 2

Математическая теория, удовлетворяющая системе аксиом, называется ее моделью (интерпретацией, реализацией).

Пусть W – некоторая система аксиом, которая является основанием аксиоматической теории Т, а Т ₁ – непротиворечивая теория, на которой строим модель системы аксиом W, а значит, и теории Т.

Сначала определяют объекты и отношения теории Т ₁. Затем составляют словарь модели, показывающий, какие объекты и отношения теории Т ₁ ставят в соответствие основным объектам и отношениям теории Т, вводимым системой аксиом W. Далее показывают, что все аксиомы системы W выполнимы. Если это удается сделать, то говорят, что модель теории Т построена в теории Т ₁. Реализация всех аксиом ведет к реализации всех теорем как логических следствий и возможности доказательства теорем теории Т на языке теории Т ₁.

Если в теории Т имеется противоречие, т.е. доказаны две теоремы, отрицающие одна другую, то такие теоремы должны быть соответственно и в Т ₁, что невозможно, так как теория Т ₁ непротиворечива. Проверка непротиворечивости теории т с помощью построения модели условна: если теория Т ₁ непротиворечива, то непротиворечива и построенная на ней теория Т.

Докажем, что система аксиом Вейля трехмерного евклидова пространства непротиворечива. Для этого построим ее модель, выбрав в качестве теории Т ₁ теорию (арифметику) действительных чисел. Таким образом, в качестве числовой системы выступает система действительных чисел. Это сложная математическая теория, которая подробно рассматривается в курсах алгебры и теории чисел. В курсе геометрии будем считать ее заданной со всеми ее свойствами.

Итак, W – система аксиом Вейля, состоящая из 17 аксиом:

.

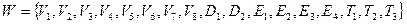Основные объекты: точка, вектор.

Основные отношения: сложение векторов, умножение вектора на действительное число, скалярное произведение векторов, отношение связи точек с векторами.

Составим словарь модели (интерпретационный словарь).

Точку понимаем как упорядоченную тройку действительных чисел , вектор – так же 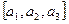. Для отличия точки от вектора используем круглые и квадратные скобки соответственно. Соответствие между основными понятиями и их интерпретациями обозначим стрелкой «®»:

точка Х ® ;

вектор ® ;

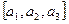нулевой вектор ® ;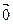

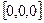противоположный вектор –® ;

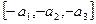сумма векторов и ® +=;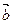

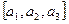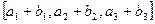произведение вектора на число a ® a =;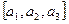

скалярное произведение и ® ×=;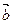

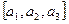связь точек с векторами: если А ® 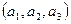, В ® ,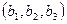

то ® .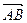

Докажем, что при указанных соглашениях выполняются все 17 аксиом.

Аксиома V ₁. Для любых векторов и 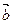с ложение коммутативно, т.е. .

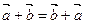Доказательство.

+===+.

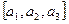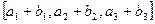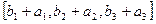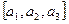Коммутативность сложения векторов следует из коммутативности сложения действительных чисел.

Проверьте самостоятельно выполнимость аксиом группы V ₂– V ₈ группы I аксиом линейного пространства.

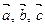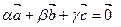Аксиома D ₁. Существуют такие три вектора , что Û .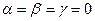

Доказательство. Рассмотрим векторы 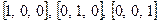. Запишем равенство 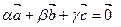на языке модели 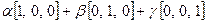=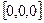. Тогда =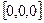. Откуда следует, , т.е. 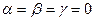, что и требовалось доказать.

Аксиома D ₂. Для любых четырех векторов 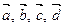существуют такие числа a, b, g, d, что выполняется равенство 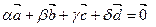, причем числа a, b, g, d одновременно не равны 0, т.е. (a, b, g, d)¹(0,0,0,0).

Доказательство. Рассмотрим векторы 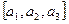, , , . Запишем равенство 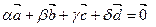на языке модели:

a 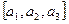+ b + g + d =.

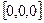Из равенства для «координат» следует:

.

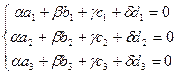Система однородных уравнений совместна и допускает ненулевое решение (объясните, почему?). Отсюда следует выполнимость аксиомы D ₂.

Таким образом, аксиомы группы II (размерности) выполнимы.

Проверим аксиомы группы III (метрические или скалярного умножения).

Аксиома Е ₁. Для любых векторов и 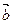скалярное умножение коммутативно, т.е. .

Доказательство. Рассмотрим векторы 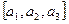и .

×===×.

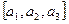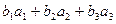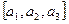Коммутативность скалярного умножения векторов следует из коммутативности умножения действительных чисел.

Проверьте самостоятельно выполнимость аксиом Е ₂– Е ₄ группы III.

Проверим выполнимость аксиом группы IV (связи точек и векторов).

Аксиома Т ₁. Существует хотя бы одна точка, т.е. Е ¹Æ.

Для доказательства возьмем любую тройку чисел, например (5, 0, 7)¹(0, 0, 0). Такая точка существует.

Аксиома Т ₂ (аксиома откладывания вектора от точки). Для любой точки А и любого вектора 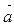существует единственная точка В такая, что .

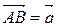Доказательство. Пусть даны точка 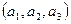и вектор 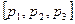, а точка 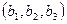– искомая. Тогда должно выполняться равенство:

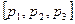=, т.е. 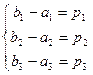, откуда .

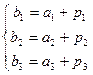Числа 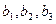однозначно находятся из полученной системы. Аксиома Т ₂ выполнима.

Аксиома Т ₃ (аксиома треугольника). Для любых точек А, В, С выполняется равенство .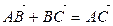

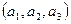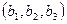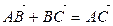Доказательство. Рассмотрим точки , , . Запишем равенство на языке модели:

+=.

Это справедливо, так как 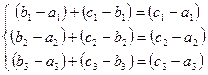(объясните, почему?).

Вывод. Проверив выполнимость всех аксиом, мы построили модель системы аксиом Вейля трехмерного евклидова пространства в арифметике действительных чисел. Эта модель называется арифметической. Ее существование доказывает, что система аксиом Вейля непротиворечива, если непротиворечива теория действительных чисел.

После построения такой модели можно сформулировать все понятия евклидовой геометрии на языке модели. Например, прямая 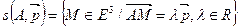на языке модели определяется следующим образом: прямой с начальной точкой 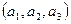и направляющим вектором 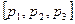¹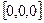называется множество точек

или , .

Получили параметрические уравнения прямой, которые изучались в курсе аналитической геометрии.

Дата добавления: 2014-01-05