Параллельность прямых и плоскостей

Отношение параллельности прямых и плоскостей вводится через их направляющие подпространства: одномерное линейное векторное пространство L ¹ для прямой и двумерное линейное векторное пространство L ² для плоскости:

, .

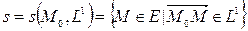Определение 7.

Две прямые (две плоскости) называются параллельными, если их направляющие подпространства совпадают. Прямая, называется параллельной плоскости, если направляющее подпространство прямой является подмножеством направляющего подпространства плоскости.

На языке символов определение запишется следующим образом:

1) , , 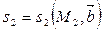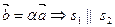(рис. 12 а);

2) , ,

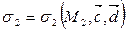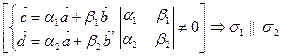
(рис. 12 б);

3) , , 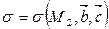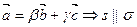(рис. 12 в).

Дата добавления: 2014-01-05