Moments of inertia of continuous bodies

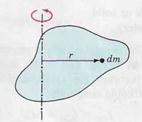
When the distribution of mass of a system of particles is continuous, the discrete sum 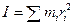is replaced by an integral. We have to sum the contributions of infinitesimal mass elements dm shown in Fig. 6.4, each of which contributes dI = r ² dm to the moment of inertia. The mass element should be chosen such that all the particles on it are at the same perpendicular distance from the axis. The moment of inertia of the whole body takes the form

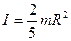(6.3)

FIGURE 6.4

Keep in mind that here the quantity r is the perpendicular distance to an axis, not the distance to an origin. To evaluate this integral, we must express m in terms of r. The following examples illustrate how this is done.

Дата добавления: 2014-01-05