Simple harmonic oscillation

Major Points

CONSERVATION OF ANGULAR MOMENTUM

From Eq. 12.9 we infer the following:

If τ _EXT = 0, then L = constant

If the net external torque on a system is zero, the total angular momentum is constant in magnitude and direction.

This is the principle of the conservation of angular momentum. We begin by applying it to the special case of rigid bodies rotating about fixed axes, in which case the angular momentum is L = Iω. The condition L_f = L_i, then takes the form

(Rigid body) I_fω_f = I_iω_i (6.15)

If a body is able to redistribute its mass and thereby change its moment of inertia, its angular velocity will also change. Although the body changes shape, we are justified in using a rigid body formula if, at any given time, all the particles have the same angular velocity.

CHAPTER 7

Oscillation

1. In a simple harmonic oscillation the amplitude is constant and the period is
independent of the amplitude.

2. Simple harmonic motion occurs when the restoring force is proportional to
the displacement from equilibrium and in the opposite direction.

3. The variation of the kinetic and potential energies with time and with position.

4. The behavior of simple pendulums, physical pendulums, and torsional pendulums.

Any motion or event that repeats itself at regular intervals is said to be periodic. In some periodic motions a body moves back and forth along a given path between two extreme positions. Such periodic motions are examples oscillation. In general, an oscillation is a periodic fluctuation in the value of physical quantity above and below some central or equilibrium value.

We begin by discussing examples of simple harmonic oscillation which is an oscillation that occurs without loss of energy. If friction, or some other mechanism, causes the energy to decrease, the oscillations are said to be damped. Finally, we discuss the response of a system to an external driving force that varies sinusoidally in time. Such forced oscillations exhibit the phenomenon of resonance when the frequency of the driving force is close to the natural frequency of oscillation of the system.

A convenient system for studying oscillations is a block attached to a spring. To see how the displacement from equilibrium, x, varies with time, we can record the motion on a strip of paper that moves at a constant speed. We find that a sinusoidal pattern is traced out. In the absence of friction, the block oscillates between the extreme values x = +A and x = -A, where A is called the amplitude of the oscillation. The displacement from equilibrium is given by

where ω, measured in rad/s, is called the angular frequency, rather than the angular velocity, since it does not refer to the rotation of something physical. One cycle corresponds to 2π radians and is completed in one period, T. Therefore, 2π = ωT, or

(7.1)

where f= 1/T, called the frequency, is measured in s^–1 or hertz (Hz). In Fig. 15.1 the block was at x = 0 at t = 0. In general this will not be the case, so we write

The argument is called the phase, while is called the phase constant (or in some contexts, the phase angle). Both the phase and the phase constant are measured in radians. The specific values of A and φ in a given problem are determined by the values of x and the velocity, v = dx/dt, at some specific time, such as t = 0. φ

Any system in which the variation in time of a physical quantity is given by Eq. 15.2 is called a simple harmonic oscillator. A simple harmonic oscillator has the following characteristics:

1. The amplitude A is constant. (The oscillation is simple.)

2. The frequency and period are independent of the amplitude: Large oscillations have the same period as small ones. (The property of isochronism.)

3. The time dependence of the fluctuating quantity can be expressed in terms of a sinusoidal function of a single frequency. (The oscillation is harmonic.)

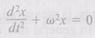(7.2)

This form of differential equation characterizes all types of simple harmonic oscillation—mechanical or nonmechanical. The techniques we develop to deal with this equation may be applied to all examples of simple harmonic oscillation. Equation 7.1 is a solution of this differential equation.

The term simple harmonic motion (SHM) is applied to mechanical examples of simple harmonic oscillation. For SHM to occur, three conditions must be satisfied. First, there must be a position of stable equilibrium. Second, there must be no dissipation of energy, for example, due to friction. Third, as we can see by writing Eq. 15.5 in the form

the acceleration is proportional to the displacement and opposite in direction.

Дата добавления: 2014-01-05