The block-spring system

We begin by considering the dynamics of a block that is oscillating at the end of a massless spring. We assume that the net force acting on the block is that exerted by the spring, which is given by Hooke's law:

F_sp = -kx

where x is the displacement from the equilibrium position. When x is positive, Fsp is negative, the force is directed to the left. When x is negative, F_sp is positive, the force is directed to the right. Thus, the force always tends to restore the block to its equilibrium position x = 0. Newton's second law (F = ma) applied to the block is –kx = ma, which means

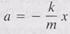
The acceleration is directly proportional to the displacement, but is in the opposite direction, as is required for SHM. Since a = d²x/dt², we have

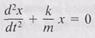(15.6)

This differential equation is another way of writing Newton's second law. When Eq. 15.6 is compared with Eq. 15.5, we see that the block-spring system executes simple harmonic motion with an angular frequency

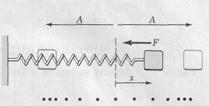
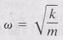(15.7) or a period

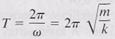(15.8) Period of a block-spring system

As is required for SHM, the period is independent of the amplitude. For a given spring constant, the period increases with the mass of the block: A more massive block oscillates more slowly. For a given block, the period decreases as к in­creases: A stiffer spring produces quicker oscillations.

FIGURE 15.4

Дата добавления: 2014-01-05