Rotational dynamics of a rigid body (fixed axis)

TORQUE

We now turn our attention to rotational dynamics. When Newton's second law is applied to the rotational motion of a body, the analysis is greatly simplified by the introduction of a quantity called torque. As we will see, torque is the rotational analog of force: Force causes linear acceleration; torque causes angular accelera­tion.

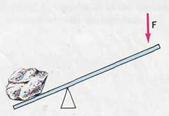
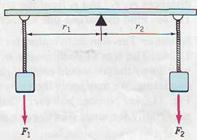
In order to lift a stone by using a lever, as shown in Fig. 6.5, a force is required. The effectiveness of the force depends both on its direction and where it is applied relative to the pivot point. The "turning ability" of a force about an axis or pivot is called its torque. Figure 6.6 shows two unequal weights hanging on either side of a balanced rod. The forces act at distances r₁ and r ₂ from the pivot. The condition for the rod to be balanced is r ₂ /r ₁ = F₁/F₂, or

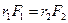
FIGURE 6.5	FIGURE 6.6

The product rF is the torque of the force F about the pivot. Clearly, the torque increases linearly with distance from the pivot.

Leonardo da Vinci extended this concept of torque to cases in which the force does not act perpendicular to the lever. In Fig. 11.23 a force is used to turn a rod pivoted at one end. The component of the force parallel to the rod just pulls at the pivot, so only the perpendicular component contributes to the turning effect. Thus, the torque is 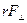. Da Vinci pointed out that one could also consider the force as acting at the effective distance 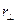, called the lever arm. The lever arm is the perpendicular distance from the origin (pivot or axis) to the line of action of the force—which is obtained by extending its arrow either forward or backward. The torque is also 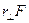. From the figure we see that 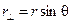and , so the two expressions, 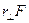and 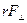, are equivalent:

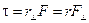(6.4)

The torque of a force F that acts at a distance r from the origin is defined to be

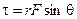(6.5) Torque

where θ is the angle between the vectors r and F. The SI unit of torque is N·m. Although this has the same dimensions as energy, these two concepts are unre­lated. We will see in Chapter 12 that whereas energy is a scalar, torque is a vector. Since this chapter is restricted to the special case of a rigid body rotating about a fixed axis, we may postpone having to deal with the full vector nature of torque. Instead, we specify its sense rather than its proper direction. We may adopt the convention that a torque tending to produce a counterclockwise rotation is positive, as indicated by the circular arc and plus sign in Fig. 11.23. In any case, the choice must be consistent with the convention chosen for angular velocity.

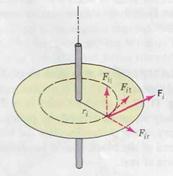
FIGURE 6.7

Figure 6.7 shows a rigid body rotating about a fixed axis, where F _i is the net external force on the i th particle of mass m_i. Any component of F _i parallel to the axis is counteracted by the reaction of the supports. For the same reason any radial component is also balanced. Only the component F_{i t}, tangential to the circular path, will accelerate the particle. We may relate the linear acceleration of the particle to the angular acceleration of the body with Eq. 11.11, a_t = αr. Thus, the second law, F _i = m a _i, becomes

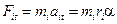
The torque on the particle about the axis is

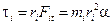
When we add the torques on all the particles, we find

(Rigid body, fixed axis) τ = Iα (6.6)

where 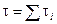is the net external torque on the body and 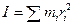is the moment of inertia about the given axis.

Equation 6.6 has the same form as F = Ma. Thus, torque is the rotational analog of force: Torque causes angular acceleration and force causes linear accel­eration. Notice, however, that Eq. 6.6 is not a vector equation. We assert without proof that it is valid in two situations:

(i) The axis is fixed in position and direction.

(ii) The axis passes through the CM and is fixed in direction only.

FIGURE 6.8

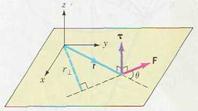
6.5 THE TORQUE VECTOR

In Eq. 6.5 the magnitude of a torque was defined as 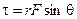, where θ is the angle between the vectors r and F. Torque is in fact a vector quantity, and so its direction must be specified relative to a coordinate system. We recall the defini­tion of the vector product,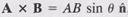, and note that its magnitude has the same form as that of τ. The definition of torque as a vector quantity is

τ = r x F = rF sinθ ň (6.7)

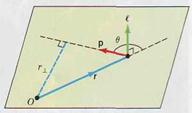
Where ň is a unit vector normal to the plane of r and F. Its direction is given by the right-hand rule, as shown in Fig. 6.8. Since the position vector r is measured relative to an origin O, the torque is also measured relative to this point. (In contrast, the r that appears in the moment of inertia formula is the perpendicular distance to an axis of rotation. In many instances the origin is chosen to lie on the axis.)

FIGURE 6.9

Дата добавления: 2014-01-05