Пример 1.2

В функции алгебры логики заданный таблицей № 1 исследовать на фиктивность аргумент 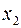. Согласно пункту №1 алгоритма область определения функции 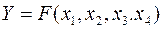разбиваем на два подмножества: 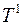и :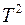

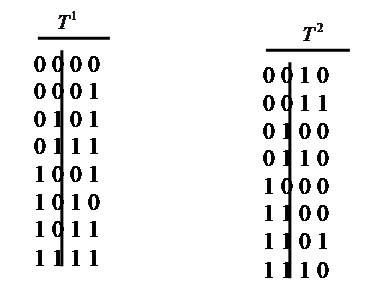В соответствии с пунктом №2 в обоих подмножествах 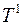и 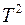вычёркивается столбец, соответствующий аргументу, анализируемому на существенность. Следуя условию, нам необходимо вычеркнуть второй столбец подмножеств. В подмножествах 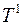и 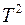после вычёркивания второго столбца появились одинаковые наборы <000>, <011>, <101>, <110>. Следовательно, аргумент 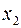является фиктивным.

Теорема 1.1:

Число функций алгебры логики зависящих от 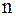аргументов конечно и равно .

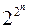Доказательство:

Пусть функция алгебры логики зависит от 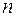аргументов. Составим для функции таблицу истинности (таблица 2).

Таблица 1.2.

Таблица истинности функции, зависящей от 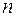аргументов.

№ п/п				…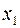
				…
				…
				…
…	…	…	…	…	…	…
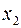
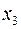
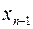
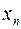
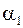
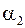
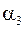
k				…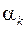

В таблице значения функции обозначены переменными 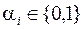, 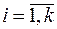. Количество функций алгебры логики совпадает с числом наборов 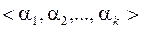. Число таких наборов составляет 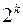. Но 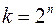, следовательно .

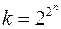Дата добавления: 2014-01-05