Элементарные функции алгебры логики

Рассмотрим функцию алгебры логики , зависящую от 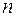аргументов.

Допустим, что 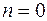, т.е. функция не содержит ни одного аргумента. Определим количество функций алгебры логики, не содержащих аргументов. Согласно теореме 1 это количество составит 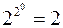. Таким образом, существует две функции алгебры логики, не содержащие аргументов. Эти функции называются константам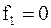и: и .

Допустим, что , т.е. имеем класс функций алгебры логики, зависящих от одного аргумента и имеющих вид: 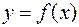. Определим количество функций алгебры логики такого класса в соответствии с теоремой 1 это количество будет равно 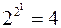. В множестве этих функций найдутся функции как существенно зависящие от своего аргумента, так и функции, несущественно зависящие от него. Представим это множество функций посредством таблицы истинности (таблица 3). 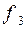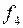Таблица демонстрирует, что функции и несущественно зависят от своего аргумента (эти функции помечены в третьей строке таблицы сочетаниями «н/с»), а функции и существенно зависят от аргумента и помечены буквой «с». При этом значение функции 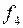повторяет значение аргумента . Функция же принимает значения, обратные значению аргумента и носит название «не »: .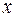

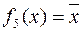Таблица 1.3

Функции алгебры логики, зависящие от одного аргумента

№ п/п
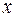
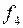
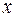
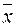
		н/с	с	с	н/с

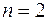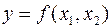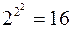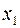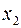Рассмотрим множество функций, зависящих от двух аргументов, т.е. : . Количество этих функций составляет . Среди этих функций найдутся функции как существенно, так и несущественно зависящие от аргументов и . Рассмотрим только те функции алгебры логики вида 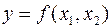, которые существенно зависят от своих аргументов. Эти функции представлены в виде таблицы истинности (Таблица 4).

Таблица 1.4.

Таблица истинности элементарных функций алгебры логики

	(&)	(~)	(+)	↓	/	→

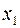
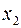
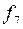
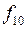
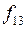
В таблиуе 4 функции означают следующее:

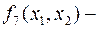функция логического сложения, дизъюнкция (функция «или»): ;

функция логического умножения, конъюнкция (функция «и»): ;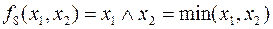

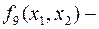эквиваленция, функция принимает значение 1 если значения обоих аргументов одинаковы: ;

сложение по модулю2, принимает значение 1 при различных значениях аргументов: ;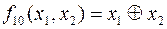

функция Вебба, принимает значения, обратные дизъюнкции: ;

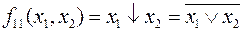штрих Шеффира – принимает значения, обратные конъюнкции:

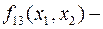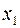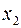импликация: (читается, если , то , или 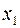влечет за собо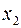й , или 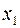имплицирует ).

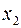Дата добавления: 2014-01-05