
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные операции над множествами
|
|
|
|
Множества. Способы задания множеств.
ТЕОРИЯ МНОЖЕСТВ И ОТНОШЕНИЙ
Начало теории множеств было положено в ХIХ веке работами Больцано, Дюбуа, Реймона, Дедекинда, посвящёнными числовым множествам и множествам функций. Но основателем теории множеств является Георг Кантор, рассмотревший в своих работах множества произвольных элементов. В 1971-1883 гг. он опубликовал научные работы, в которых изложено практически всё современное содержание теории кардинальных чисел, порядковых чисел и теории вполне упорядоченных множеств. Хотя основные положения и обобщения изложенной теории содержали немало противоречий, позволяющих строить антиномии теории множеств, это был, всё же, очень важный шаг. Эти противоречия были преодолены Цермело посредством работ, опубликованных в 1904-1908 гг. и содержащих первую систему аксиом теории множеств. Этих аксиом оказалось достаточно, чтобы получить важные для математики научные результаты, не позволяющие строить известные антиномии. Тесная связь между теорией множеств и философией математики породило немало дискуссий о природе антиномий и аксиоматизации теории множеств. Фундаментальные проблемы философии математики, такие как понятие существования в математике, аксиоматические версии описания действительности, необходимость доказательств непротиворечивости и средства, допустимые в таких доказательствах, нигде не были выяснены лучше, чем в этих дискуссиях. Недоверие к теории множеств прекратилось и основные положения вновь созданной теории стали повсеместно использоваться во всех областях математики.
Основным понятием теории множеств является множество и отношение быть элементом. Это понятие по мере развития теории претерпело значительные изменения. В начальный период развития теории множеств, во времена так называемой «наивной» теории множеств, пользовались интуитивным понятием множества. В рамках этого понятия слово «множество» имело неопределённое значение. В частности, такую позицию занимал создатель теории множеств Георг Кантор.[2]
|
|
|
Но такое положение долго не продержалось.
Под множеством будем понимать совокупность элементов, объединённых некоторым признаком или свойством. Например, множество журналов, множество статей в журнале, множество студентов в группе, на факультете и т.д. Принадлежность некоторого элемента 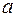 множеству
множеству 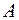 будем записывать как
будем записывать как  , а непринадлежность ─
, а непринадлежность ─  . Множество можно задать тремя способами. Первый способ ─ перечисление элементов. В этом случае обозначения элементов заключают в фигурные скобки в виде записи
. Множество можно задать тремя способами. Первый способ ─ перечисление элементов. В этом случае обозначения элементов заключают в фигурные скобки в виде записи 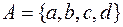 или
или  или
или  . Второй способ ─ использование характеристического предиката (характеристического свойства). Характеристический предикат ─ это некоторое условие в виде логического утверждения, которое возвращает логическое значение из множества {0,1}. Во втором случае используется запись
. Второй способ ─ использование характеристического предиката (характеристического свойства). Характеристический предикат ─ это некоторое условие в виде логического утверждения, которое возвращает логическое значение из множества {0,1}. Во втором случае используется запись 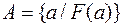 , означающая, что множество
, означающая, что множество 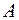 состоит из элементов, обладающих свойством
состоит из элементов, обладающих свойством 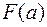 , или
, или  , означающая, что множество
, означающая, что множество 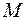 состоит из тех и только тех элементов натурального ряда чисел, которые больше 100. Характеристическое свойство записывается после знака «/». В первом случае в качестве характеристического свойства выступает указанная для этого свойства порождающая процедура
состоит из тех и только тех элементов натурального ряда чисел, которые больше 100. Характеристическое свойство записывается после знака «/». В первом случае в качестве характеристического свойства выступает указанная для этого свойства порождающая процедура 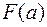 . Эта процедура описывает способ получения элементов нового множества из уже полученных элементов или каких-либо объектов. Таким образом, запись
. Эта процедура описывает способ получения элементов нового множества из уже полученных элементов или каких-либо объектов. Таким образом, запись 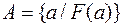 означает, что множество
означает, что множество 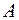 состоит из элементов, обладающих признаком
состоит из элементов, обладающих признаком 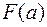 . В качестве этого признака может быть использовано уравнение:
. В качестве этого признака может быть использовано уравнение: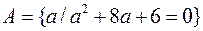 . Это означает, что множество
. Это означает, что множество 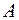 состоит из корней уравнения
состоит из корней уравнения 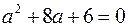 . Таким образом, если для данного элемента выполняется условие, то он принадлежит множеству, в противном случае не принадлежит. Третий способ ─ использование порождающей процедуры, которая в случае её активизации порождает некоторые объекты, являющиеся элементами определяемого множества:
. Таким образом, если для данного элемента выполняется условие, то он принадлежит множеству, в противном случае не принадлежит. Третий способ ─ использование порождающей процедуры, которая в случае её активизации порождает некоторые объекты, являющиеся элементами определяемого множества: 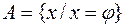 . Перечислением можно задавать только конечные множества (определение конечного множества приведено ниже).
. Перечислением можно задавать только конечные множества (определение конечного множества приведено ниже).
|
|
|
Множество, не содержащее ни одного элемента, называется пустым. Пустое множество обозначается  .
.
Множество, состоящее из всех возможных элементов, обладающих заданным признаком, называется универсальным и обозначается как 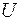 . Примером универсального множества может быть множество планет Солнечной системы
. Примером универсального множества может быть множество планет Солнечной системы 
 .
.
Понятие универсального множества чётко не определено, т.е. не корректно. Одно универсальное множество можно включить в другое множество, которое также будет универсальным.
Множество называется конечным, если число его элементов конечно. Множество называется бесконечным, если количество его элементов бесконечно.
Обычно множества обозначают прописными буквами латинского алфавита, а элементы множеств ─ строчными буквами. Множества геометрически представляются с помощью кругов Эйлера (диаграмм Венна) (рис. 2.1.). В диаграммах Венна элементы множества изображаются точками внутри круга, если они принадлежат множеству ( ), и точками вне круга, если они не принадлежат этому множеству (
), и точками вне круга, если они не принадлежат этому множеству (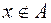 ).
).
Множества, как объекты, в свою очередь могут быть элементами других множеств. Множество, элементами которого являются множества, называются семействами или классами.
 |
Над множествами выполняются теоретико-множественные операции, в результате которых образуются новые множества: объединение, пересечение, разность, симметрическая разность, дополнение. Эти операции являются способами конструирования новых множеств из заданных множеств.
Рассмотрим два произвольных множества: множество 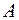 и множество
и множество 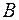 . Допустим, что каждому элементу множества
. Допустим, что каждому элементу множества 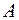 ставится в соответствие свойства
ставится в соответствие свойства 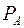 , а каждому элементу множества
, а каждому элементу множества 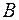 ставится в соответствие свойство
ставится в соответствие свойство 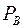 . Таким образом, каждый элемент множества
. Таким образом, каждый элемент множества 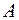 и
и 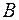 обладает соответственно свойством
обладает соответственно свойством 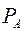 и
и 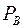 .
.
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 775; Нарушение авторских прав?; Мы поможем в написании вашей работы!