Объединение множеств

Под объединением множеств 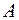и 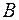будем понимать множество, обозначаемое 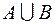и состоящее из таких элементов, которые обладают хотя бы одним из свойств: 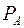или 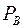. Высказывательная форма операции объединения множеств имеет вид:

.

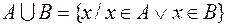Таким образом, элемент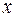принадлежит объединению множеств 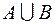тогда и только тогда, когда этот элемент принадлежит хотя бы одному из множеств: 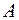или 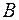. Если обозначить отношение «тогда и только тогда» символом 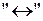, то высказывательная форма последнего выражения имеет следующий вид: 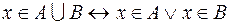. Приведённые высказывательные формы содержат логическую операцию дизъюнкции 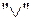, рассматриваемую нами ранее при изучении функций алгебры логики. При этом отмечалось, что операция дизъюнкции выполняется над логическими переменными 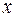, принимающими значения из двухэлементного множества 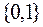: 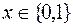. В применяемых же нами высказыватнльных формах для объединения множеств операция дизъюнкции выполняется над некоторыми выражениям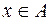и: и 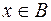. Возникает вопрос о правомерности использования логической операции над выражениями. Приведём обоснование этой правомерности в выражении 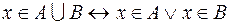. Слева и справа от знака 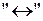стоят так называемые высказывания. В логике под высказыванием понимают любое языковое предложение, относительно которого говорят об его истинности или ложности. Таким образом, в математической логике интересуются не содержанием предложения, а его истинностным значением. В двузначной логике в качестве множества истинностных значений принято двуэлементное множество 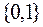, элементы которого интерпретируются как «ложь», «истина». Принятие высказываниям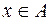и и 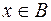значений из множества 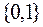и обосновывают правомерность выполнения над ними операции дизъюнкции. Применим выражение 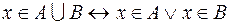для геометрической интерпретации операции объединения множеств в виде диаграммы Венна. Истинность выражения 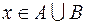, стоящего справа от знака 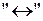, должна повлечь за собой истинность выражения 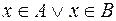, стоящего слева от этого знака. Но результат операции «дизъюнкция» между двумя переменными принимает значение «истина», если хотя бы одна переме5нная принимает значение «истина». При этом могут представиться следующие варианты:

- высказывание 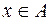принимает значение «истина», а высказывание 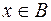принимает значение «ложь» (на рис. этому варианту соответствуют точки 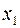и );

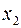- высказывание 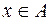принимает значение «ложь», а высказывание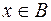принимает значение «истина» (на рис. этому варианту соответствуют точки , );

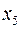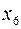- высказывание 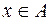и высказывание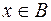принимают значение «истина» (на рис. этому варианту соответствуют точки , .

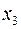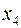Перечисленные варианты истинностных значений высказываний определяют диаграмму Венна, представленную на рис. 2.2.

Операция объединения может быть распространена и на большее количество множеств:

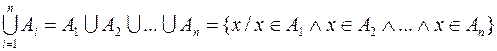
Дата добавления: 2014-01-05