Теорема

Если 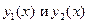- частные решения уравнения (2), то функция 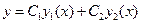является решением уравнения (2) при любых .

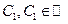Доказательство:

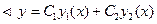
Найдем производные:

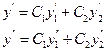
Подставим в уравнение (2):

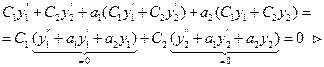
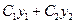- линейная комбинация решений .

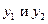Вывод: если 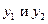- решения уравнения (2) такие, что 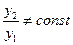, то выражение 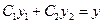является общим решением уравнения (2).

Из общего решения при любых заданных возможных начальных условиях может быть найдено частное решение, удовлетворяющее этим начальным условиям.

Пусть заданы начальные условия:

,

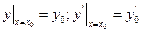причем точка 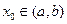,где 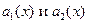константы, то может быть любой. Подставляя начальные условия в общее решение, получим систему относительно .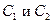

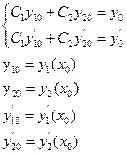
Чтобы эта система имела единственное решение при любых правых частях необходимо и достаточно, чтобы определитель системы был не равен нулю, т.е. 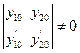(3)

Утверждение: если 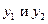такие решения, что 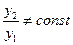, то определитель (3) не будет равен нулю ни в одной точке .

Рассмотрим теперь уравнение с правой частью.

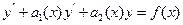(4)

Уравнение без правой части будем называть соответствующим однородному уравнению (4).

Дата добавления: 2014-01-05