Теорема (о структуре общего решения линейного неоднородного уравнения)

Общее решение уравнения (4) можно составить как сумму общего решения соответственного однородного уравнения и какого-либо частного решения данного уравнения.

Общее решение можно записать в виде:

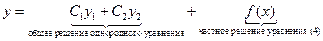
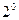. Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Рассмотрим уравнение с постоянными коэффициентами

(5), где 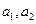- постоянные величины.

Возьмём соответствующее ему однородное уравнение (6) и найдем общее решение такого уравнения.

Введем в рассмотрение функцию

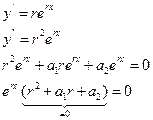
Чтобы функция 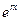являлась решением уравнения (6), надо чтобы 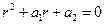(7), т.е. 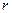будет являться решением. Уравнение (7) называется характеристическим. Чтобы составить характеристическое уравнение, нужно в данном уравнении (6) заменить 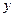единицей, а каждую производную величиной 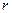в степени, равной порядку производной.

Для корней квадратного уравнения (7) возможны три случая (предполагается, что ):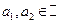

1)

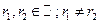
При этом оба корня могут быть взяты в качестве показателей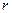в функции 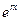, т.е имеем два частных решения 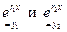(причем ясно, что 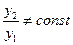). Таким образом, общее решение в этом случае выглядит так: .

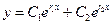Пример:

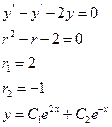
2)

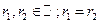
В этом случае непосредственно имеем только одно частное решение. Покажем, что в качестве второго решения можно взять функцию .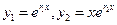

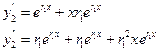
Подставим в уравнение (6):

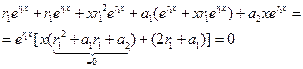
Т.к. 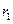- двукратный корень, то сумма корней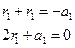

Общее решение в этом случае имеет вид:

3) - комплексно-сопряженные корни.

В этом случае общее решение можно записать так:

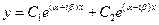, где 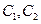- любые комплексные постоянные.

Для того, чтобы получить решение в действительной форме, воспользуемся правилом: если уравнение (6) с действительными коэффициентами имеет комплексное решение 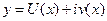, то каждая их функций является решением этого уравнения. Действительно, дифференцируя 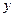и подставляя в уравнение (6), получим .

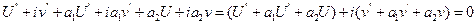Т.к. комплексная функция равна нулю, когда равны нулю ее действительная и мнимая части, получим, что оба выражения в скобках равны нулю, т.е. являются решениями уравнения (6).

Замечание: Определение Показательной функцией с мнимым показателем степени называется комплексная функция 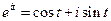- формула Эйлера, где параметр 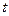- любое действительное число. Комплексная функция 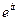дифференцируется так же, как если бы 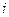было просто постоянным числом. Итак, по формуле Эйлера 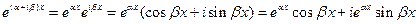, 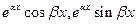- частные решения уравнения (6), причем ясно, что их отношение не равно константе.. Согласно правилу, зная два частных решения, построим общее решение:

Пример:

Дата добавления: 2014-01-05