Свойство точной верхней (нижней) грани

Как бы ни было мало число 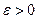, найдется 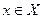такое, что 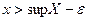и :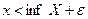

,

.

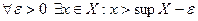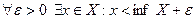J Пример 3.3. Рассмотрим множество 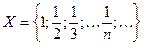, , 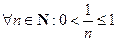то есть X ограничено.

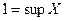(3.1),

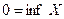(3.2).

Докажем положения (3.1) и (3.2).

1) Докажем, что число 1 является точной верхней гранью множества Х. Для этого, согласно свойству точной верхней грани, надо показать, что для любого 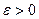найдётся натуральное число n такое, что выполняется неравенство . Этим числом является 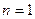, т.к. 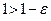. Это верно для любого 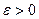. Доказано, что .

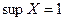2) Докажем теперь, что число 0 является точной нижней гранью множества Х. Для этого проверим, будет ли для любого 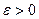выполняться неравенство 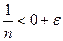или 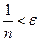. Получаем 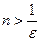. Взяв какое-нибудь натуральное число 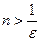, получим требуемое неравенство. Согласно свойству точной нижней грани .

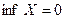Заметим, что данному множеству Х точная грань 1 принадлежит и является его наибольшим числом, а точная нижняя грань 0 не принадлежит, и в этом множестве нет наименьшего числа. J

Определение 3.4. Число 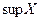называется точной верхней гранью ограниченного сверху множества X, если:

1) ,

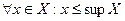2) .

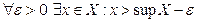Определение 3.5. Число 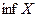называется точной нижней гранью ограниченного снизу множества X, если:

1) ,

2) .

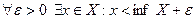Существование у любого ограниченного сверху (снизу) множества Х точной верхней (нижней) грани не является очевидным и требует доказательства.

♦ Теорема 3.1. Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху (снизу), то существует вещественное число 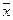(число 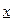), которое является точной верхней (точной нижней) гранью этого множества.

Доказательство. Докажем существование точной верхней грани.

Пусть Х ограничено сверху:

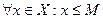(3.3).

Возможны два случая:

1°. В множестве Х есть хотя бы одно неотрицательное вещественное число.

2°. Все х являются отрицательными вещественными числами.

Рассмотрим случай 1°.

Будем рассматривать лишь неотрицательные вещественные числа .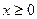

В силу (3.3) все целые части чисел x не превосходят М, а поэтому найдётся наибольшая из целых частей, которую мы обозначим через 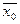. Сохраним среди неотрицательных чисел множества те, у которых целая часть равна 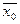и отбросим все остальные числа.

В получившимся множестве 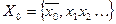рассмотрим первые десятичные знаки после запятой. Наибольший из этих знаков обозначим 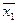и образуем множество 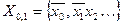. Продолжая аналогичные рассуждения, получим десятичные знаки некоторого вещественного числа .

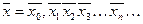Докажем, что 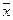, построенное таким образом, является .

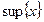Для этого достаточно доказать два утверждения:

1) ,

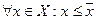2) .

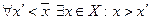Доказательство 1). 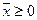, следовательно 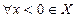удовлетворяет условию 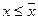. Пусть 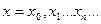– любое неотрицательное число, входящее в 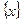. По определению числа 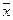: 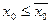. Отсюда:

либо 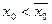, тогда 1) доказано,

либо 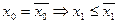, откуда, в свою очередь:

либо 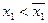доказано,

либо …

Продолжая аналогичные рассуждения мы либо докажем неравенство 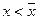, либо получаем бесконечную цепочку равенств 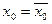, , 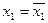,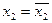..., ,..., 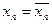из которой вытекает 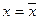. То есть 1) доказано.

Доказательство 2). Пусть 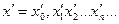– произвольное вещественное число, меньшее 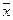(будем считать 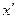неотрицательным, т.к. для отрицательного числа 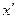неравенство 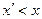справедливо для ).

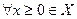По предположению 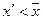, следовательно , , …, , .

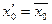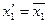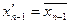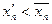С другой стороны, по построению 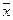всегда найдётся число 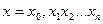: 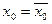, , 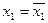…, , 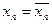но тогда .

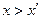Существование точной верхней грани для случая 1° доказано.

Перейдём к случаю 2°. Все x представлены в виде отрицательных бесконечных десятичных дробей. Обозначим через 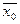наименьшую из целых частей этих дробей; через 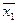наименьший из первых десятичных знаков для дробей с целой частью 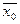и т.д. Определим таким образом отрицательное вещественное число . Аналогично случаю 1° доказывается, что . ■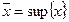

Дата добавления: 2014-01-05