Внутренняя энергия идеального газа

В модели идеального газа мы пренебрегаем взаимодействием молекул, поэтому внутренняя энергия идеального газа U равна суммарной кинетической энергии молекул W_k.

, (2.4.1)

где N – число молекул газа, 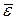- средняя кинетическая энергия молекулы, которая равна .

Тогда , откуда получим следующую формулу для вычисления внутренней энергии идеального одноатомного газа:

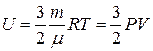. (2.4.2)

Формула (2.4.2) справедлива лишь для идеального одноатомного газа. В случае двухатомного газа в этой формуле вместо множителя 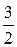должен стоять множитель . Чтобы понять, почему это так, рассмотрим сформулированный еще в XIX веке принцип равнораспределения энергии по степеням свободы. Но прежде определим, что мы понимаем под числом степеней свободы.

Число степеней свободы – это число независимых координат, которые нужно задать, чтобы однозначно определить положение молекулы в пространстве.

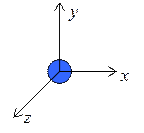
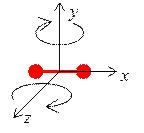
Рис. 2.4.1. Рис. 2.4.2.

На рис. 2.4.1 показана одноатомная молекула, которая имеет i = 3 степени свободы. Эти степени свободы отвечают трем независимым поступательным движениям молекулы вдоль осей x, y, z.

Для двухатомной молекулы, показанной на рис. 2.4.2 число степеней свободы равно i = 5, т.к. помимо поступательных степеней свободы существуют еще 2 вращательные степени свободы.

В общем случае число степеней свободы молекулы равно сумме числа ее поступательных степеней свободы i_пост, числа вращательных степеней свободы i_вращ и числа колебательных степеней свободы i_колеб:

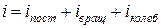. (2.4.3)

Для жесткой молекулы, имеющей три и более число атомов, число степеней свободы i = 6, т.к. для такой молекулы отсутствуют колебательные степени свободы.

Дата добавления: 2014-01-05