Розрахунок складних електричних кіл методом вузлових потенціалів. Коло з двома вузлами

Метод вузлових потенціалів заснований на застосуванні першого закону Кірхгофа і являється одним з основних методів розрахунку лінійних кіл постійного струму.

Розглянемо застосування методу на прикладі конкретного електричного кола (рис. 2.16).

Довільно задамо додатні напрями струмів в гілках. Скористаємося законом Ома для ділянки кола:

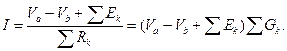
Знаючи потенціали вузлів V₁, V₂, V₃, V₄ можна записати вирази для струмів в гілках:

I₁=(V₁-V₄+E₁) G₁;

I₂=(V₁-V₄) G₂;

I₃=(V₁-V₂) G₃;

I₄=(V₄-V₂+E₄) G₄; де G₁=1/R₁; G₂=1/R₂;… – провідності гілок.

I₅=(V₂-V₃+E₅) G₅;

I₆=(V₂-V₃) G₆;

I₇=(V₄-V₃+E₇) G₇.

Як видно з виразів для струмів, їх значення залежать не від абсолютних величин потенціалів, а від їх різниці. Тому можна збільшити, або зменшити значення всіх потенціалів вузлів на одну і ту ж величину. При цьому різниця потенціалів між вузлами електричного кола буде залишатися сталою.

Змінимо потенціали всіх вузлів на таку величину, щоб потенціал одного з вузлів став рівним нулю.

Вузол, потенціал якого дорівнює нулю, називається базисним.

Нехай V₄ =0, тоді потенціали решти q-1 вузлів визначаються відносно потенціалу базисного вузла.

Визначимо потенціали V₁, V₂ та V₃, для цього складемо рівняння за І-м законом Кірхгофа для цих вузлів:

1 вузол: -І₁-І₂-І₃ =0;

2 вузол: І₃+І₄-І₅-І₆ =0;

3 вузол: І₅+І₆+І₇ =0.

Підставимо в ці рівняння вирази для струмів, враховуючи, що V₄ =0:

-(V₁+E₁)G₁-V₁G₂-(V₁-V₂)G₃=0;

(V₁-V₂)G₃+(-V₂+E₄)G₄ - (V₂-V₃ +E₅)G₅ -(V₂-V₃)G₆ =0;

(V₂-V₃+ E₅)G₅ + (V₂-V₃)G₆ +(-V₃+E₇)G₇ =0.

Перетворимо одержану систему рівнянь:

-V₁G₁-E₁G₁- V₁G₂ - V₁G₃ + V₂G₃ =0;

V₁G₃ – V₂G₃ – V₂G₄ + E₄G₄ – V₂G₅ + V₃G₅ – E₅G₅ – V₂G₆ + V₃G₆ =0;

V₂G₅ – V₃G₅ + E₅G₅ + V₂G₆ – V₃G₆ – V₃G₇ + E₇G₇ =0.

або:

V₁(G₁+G₂+G₃)-V₂G₃=-E₁G₁;

-V₁G₃ +V₂(G₃+G₄+G₅+G₆)-V₃(G₅+G₆) =E₄G₄- E₅G₅ ;

-V₂(G₅+G₆)+ V₃(G₅+G₆ +G₇) = E₅G₅+ E₇G₇.

Таким чином, одержали систему трьох рівнянь з трьома невідомими. Визначимо значення потенціалів V₁, V₂, V₃, а потім за законом Ома для ділянки кола визначимо струми в гілках.

Одержану систему рівнянь можна записати одразу на основі структури електричного кола та заданих напрямків ЕРС та джерел струму в гілках. Для цього введемо допоміжні поняття та позначення.

Власна провідність вузла – це сума провідностей гілок, що з’єднуються з цим вузлом. Позначається G_kk:

G₁₁=G₁+G₂+G₃ – власна провідність 1 вузла;

G₂₂=G₃+G₄+G₅+G₆ – власна провідність 2 вузла;

G₃₃=G₅+G₆+G₇ – власна провідність 3 вузла.

Взаємна провідність двох вузлів – це сума провідностей гілок, що з’єднують ці два вузли. Позначається G_km:

G₁₂=G₂₁=G₃ – взаємна провідність 1 та 2 вузлів;

G₂₃=G₃₂=G₅+G₆ – взаємна провідність 2 та 3 вузлів.

Вузловий струм – це алгебраїчна сума добутків ЕРС джерела кожної гілки, що з’єднуються з цим вузлом, на її провідність. Позначається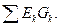

Якщо електричне коло містить джерела струму, то вузловий струм визначається так:

де J_k – струми джерел струму.

При цьому з додатнім знаком беруться ЕРС та струми, що направлені до вузла та навпаки.

Таким чином, вузлове рівняння, тобто рівняння, складене для вузла електричного кола, має наступну структуру:

- ліва частина – це алгебраїчна сума, взята із знаком «плюс», добутку потенціалу вузла та власної провідності вузла, а також взятих із знаком «мінус» добутків загальних провідностей даного вузла з рештою сусідніх вузлів електричного кола та потенціалу відповідного вузла;

- права частина – вузловий струм даного вузла.

Наприклад, вузлове рівняння для k -го вузла:

V_k G_kk -V₁ G_k1 - V₂ G_k2 -…- V_m G_km =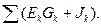

Метод вузлових потенціалів найбільш доцільно застосовувати, коли кількість вузлів набагато менша кількості незалежних контурів, тобто
(q-1)<n.

Особливо ефективний цей метод для розрахунку електричних кіл з двома вузлами. В цьому випадку складається лише одне вузлове рівняння.

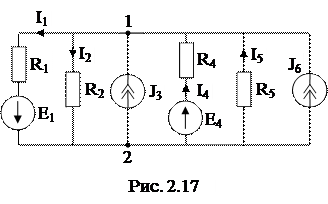
Розглянемо електричне коло (рис. 2.17).

Виконаємо аналіз кола: p =6, q =2, n=p-(q-1) =5, q < n.

Приймемо V₂ =0, тоді вузлове рівняння для вузла 1 запишеться в вигляді:

V₁ (G₁+G₂+G₄+ G₅)= - E₁ G₁+J₃+E₄ G₄- J₆.

Звідси: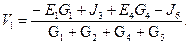

За законом Ома для ділянки кола визначаємо струми в гілках:

; .

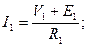
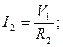
В загальному випадку потенціал одного з вузлів електричного кола з двома вузлами визначається за формулою:

.

Якщо в електричному колі є вітка, що має тільки джерело ЕРС, то число вузлових рівнянь можна зменшити. Для цього потенціал першого вузла цієї вітки приймаємо рівним нулю, тоді потенціал другого вузла цієї вітки буде дорівнювати ЕРС. Для інших вузлів складаємо звичайні вузлові рівняння (див. задачу № 9).

Дата добавления: 2014-01-05