Метод еквівалентного генератора

Даний метод застосовується дл9я розрахунку струму в одній гілці складного електричного кола, а також для визначення залежності струму від опору гілки.

Розглянемо електричне коло (рис. 2.18).

Визначимо струм I₄ та встановимо залежність.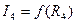

Для цього розіб’ємо складне коло на дві частини:

І частина – гілка, в якій визначається струм, тобто виділена гілка;

ІІ частина – вся решта кола, тобто двополюсник.

Двополюсники бувають активні (що мають джерела електричної енергії) та пасивні (що не містять джерел електричної енергії).

Метод еквівалентного генератора оснований на теоремі про активний двополюсник, яка визначається так:

«Будь-який активний двополюсник по відношенню до виділеної гілки можна розглядати як еквівалентний генератор з внутрішнім опором R_вт та ЕРС, що дорівнює напрузі холостого ходу U_XX між вхідними затискачами двополюсника при розімкненій виділеній гілці».

Тоді вихідна схема прийме вигляд, зображений на (рис. 2.19). Тут струм І₄ можна визначити за законом Ома:

.

В загальному випадку

.

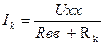Розглянемо послідовність розрахунку струму в виділеній гілці.

1. Визначаємо напругу холостого ходу U_xx, для чого зобразимо розрахункову схему, в якій розімкнемо виділену гілку (рис. 2.20).

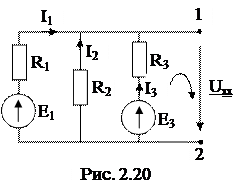Вкажемо напругу холостого ходу на затискачах виділеної гілки (вона, звичайно, співпадає з напрямом струму).

Задамося додатнім напрямом струмів в гілках.

Складаємо рівняння за другим законом Кірхгофа для контуру, в який входить U_xx:

I₃^`R₃+U_xx=E₃,

звідси U_xx= E₃- I₃^`R₃.

Визначимо струм I₃, для цього використаємо метод вузлових потенціалів, так як маємо схему з двома вузлами.

Нехай V₂ = 0, тоді V₁ (G₁+G₂+G₃)=E₁ G₁+E ₃G₃.

Звідси: 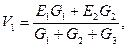а струм дорівнює: I₃^` =(V₂ – V₁+ E₃) G₃.

Одержимо кінцевий вираз для напруги U_xx:

U_xx= E₃ – V₂+ V₁ - E₃= V₁ –V₂.

2. Визначимо внутрішній опір R_вт відносно затискачів 1 та 2. Для цього на розрахунковій схемі (рис. 2.21) видалимо всі джерела електричної енергії. При цьому точки підключення ідеальних джерел ЕРС замикаються накоротко, а гілки з ідеальними джерелами струму видаляються.

Тоді:

.

3. Визначимо струм в виділеній гілці:

.

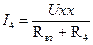4. Зміняючи R₄ від 0 до ∞, побудуємо залежність 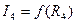(рис. 2.22).

2.10. Принцип та метод накладання

Принцип накладання (суперпозиції) полягає в тому, що струм в будь-якій гілці електричного кола, викликаний дією декількох джерел, дорівнює сумі струмів в цій гілці, що викликані кожним джерелом окремо (при рівності нулю решти ЕРС або струмів джерел):

де 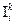– струм в і -тій гілці, викликаний дією k -го джерела.

Принцип суперпозиції можна застосовувати лише до лінійних електричних кіл.

Для доказу методу накладання скористаємось системою контурних рівнянь, що визначають контурні струми в електричному колі рис. 2.15, яка була одержана в методі контурних струмів.

Згідно з теорією визначників, контурні струми можуть бути одержані за формулами:

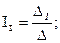
; де

Δ_ІІІ=.

Δ_І, Δ_ІІ, Δ_ІІІ – часткові визначники системи, що дорівнюють:

	ΔІІ =;

Якщо розкласти визначники Δ_І, Δ_ІІ, Δ_ІІІ по елементах стовпців, то

вирази для контурних струмів приймуть такий вигляд:

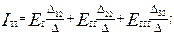
де – алгебраїчні доповнення (k =1,2,3; m =1,2,3), одержані з головного визначника шляхом викреслювання у ньому k- го рядка та m -го стовпця та множенням одержаного визначника на .

Вирази для контурних струмів можна записати в наступному вигляді:

; ; ;

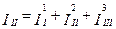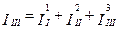де – частина контурного струму першого контуру, що викликана першим джерелом ЕРС і т.д.

Таким чином, одержані вирази для контурних струмів представляють собою аналітичний вираз метода накладання для контурних струмів. Але контурний струм дорівнює дійсному струму, якщо гілка входить лише в один контур. Ця умова завжди може бути забезпечена відповідним вибором незалежних контурів.

Отже, метод накладання справедливий і для дійсних струмів гілок кола.

Розглянемо розрахунок складного електричного кола методом накладання на конкретному приладі (рис. 2.23).

Порядок розрахунку:

1. Визначимо струм в гілках кола при наявності лише ЕРС Е₁, при цьому вважаємо, що Е₂ = 0.

Зобразимо відповідну електричну схему (рис. 2.23,б).

Струми в електричному колі в цьому випадку будуть дорівнювати

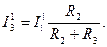
2. Визначимо струми в гілках кола при наявності лише ЕРС Е₂, при цьому вважаємо, що Е₁ = 0.

Зобразимо відповідну електричну схему (рис. 2.23,в).

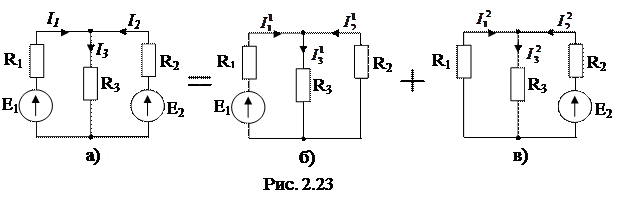
Струми в електричному колі в цьому випадку дорівнюватимуть:

3. На основі принципу накладання визначимо дійсні величини струмів в вихідній схемі:

; ; .

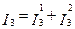Метод накладання трохи громіздкий та не зручний для розрахунку. Разом з тим в ряді випадків застосування цього методу дозволяє швидко визначити струм в одній гілці, дослідити вплив зміни однієї з ЕРС. на зміну струмів в гілках, а також вирішити деякі інші задачі.

Дата добавления: 2014-01-05