Декартово произведение множеств

Понятие разбиения множества на классы с помощью одного, двух, трех свойств

Понятия множества и операций над множествами позволяют уточнить наше представление о классификации – действии распределения объектов по классам.

Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса – четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы Х₁, Х₂, …, Хn,…, если:

1) подмножества Х₁, Х₂, …, Хn,… попарно не пересекаются;

2) объединение подмножеств Х₁, Х₂, …, Хn, … совпадает с множеством Х.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим,. что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.

N N

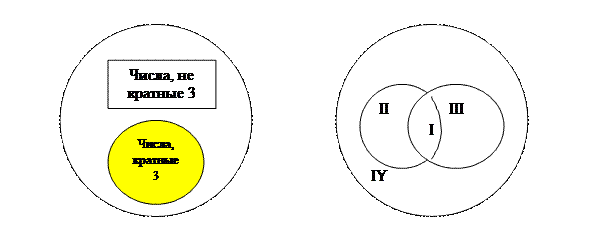
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающий этим свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А – подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого. Проанализируем получившийся рисунок (справа). Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей – на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратных 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IY – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

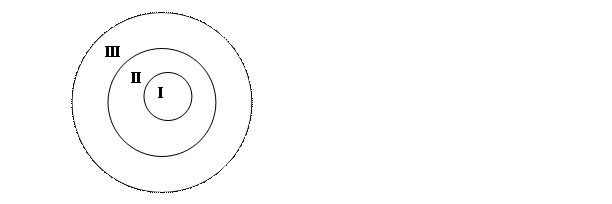
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи двух таких свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса: I – класс чисел, кратных 6; II – класс чисел, кратных 3; но не кратных 6; III - класс чисел, не кратных 3.

Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b – второй координатой (компонентой) пары.

Пары (а; b) и (с; d) равны в том и только в том случае, когда а = с и b = d.

В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая компонента – множеству В. Если мы перечислим все такие пары, то получим множества:

{(1; 3), (1; 5) (2; 3), (2; 5), (3; 3), (3; 5)}.

Видим, что, имея два множества А.и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.

Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:

А х В = {х; у) / х ∈ А и у∈ В}.

Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А х В и В х А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.

Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:

(А∪В) х С = (А х С) ∪ (В х С),

(А / В) х С = (А х С) / (В х С).

Доказывать эти свойства мы не будем, но проверить их можно на конкретных примерах.

Выясним теперь, как можно наглядно представить декартово произведение множеств.

Если множества А и В конечны и содержат небольшое количество элементов, то его можно изобразить при помощи графа или таблицы. Например, декартово произведение множеств

А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке.

А В

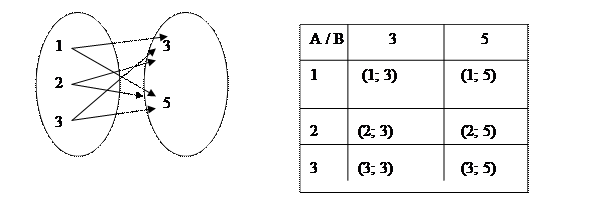
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изобразить на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение выше названных множеств на координатной плоскости будет выглядеть так:

1 2 3

Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В – на оси Оу.

Такой способ наглядного изображения декартова произведения множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.

В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367 – это упорядоченный набор из трех элементов, а запись слова «математика» - это упорядоченный набор из 10 элементов.

Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10.

Рассматривают в математике и декартово произведение трех, четырех и вообще n множеств.

Определение. Декартовым произведением множеств А₁, А₂, …, Аn называется множество всех кортежей длины n, первая компонента которых принадлежит множеству А₁, вторая – множеству А₂, …, n-я - множеству Аn.

Декартово произведение множеств А₁, А₂, …, Аn обозначают так:

А₁ х А₂ х …х Аn.

Дата добавления: 2014-01-06