Приведение уравнения кривой 2-го порядка к каноническому виду

Общее уравнение кривой 2-го порядка имеет вид:

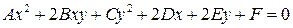(1), где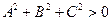

Подходящим преобразованием поворота 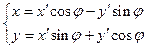можно добиться того, чтобы в новых коородинатах коэффициент B' = 0. Тогда уравнение (1) запишется в виде:

(2)

С помощью преобразования вида 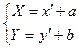уравнение (2) можно привести к одному их 3-х основных канонических типов:

I.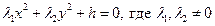

II.

III.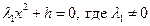

Классификация кривых 2-го порядка

В зависимости от соотношения знаков в коэффициентах уравнений основных канонических типов I-III, возникают следующие канонические уравнения:

1. Эллипс

2 Мнимый эллипс

3. Пара мнимых пересекающихся прямых

4. 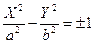Гипербола

5. Пара пересекающихся прямых

6. 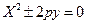Парабола

7. 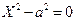Пара параллельных прямых

8. Пара мнимых параллельных прямых

9. Пара совпадающих прямых

Заметим, что кривые 1-5 получаются I-го основного канонического типа, кривая 6 – из II-го, а кривые 7 - 9 - из III-го основного канонического типа.

Дата добавления: 2014-01-06