Закон равнораспределения энергии по степеням свободы

Рассмотрим двухатомный газ. Молекулы газа испытывает столкновения друг с другом. Выделим произвольную молекулу. Будем считать, что импульсы, получаемые каждым атомом данной молекулы при ее столкновениях, не зависят друг от друга. (Момент столкновения столь краток, что действующие в молекуле межатомные силы не успевают повлиять на эти импульсы.) Полная кинетическая энергия молекулы складывается из кинетических энергий обоих атомов, и вместо (1.22) в сумме получается .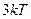

Движение центра масс молекулы дается выражением, аналогичным (1.13):

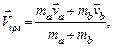(4.13)

где индексы а и b относятся к двум атомам.

Усредним квадрат скорости (4.13) в моменты времени сразу после столкновений, когда еще можно считать, что скорости каждого атома не зависят друг от друга:

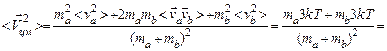
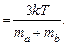(4.14)

(Скалярное произведение в числителе усредняется до нуля из-за указанной независимости.) Отсюда

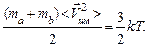(4.15)

Так как между столкновениями 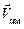не меняется, этот результат остается справедливым и во все остальные моменты времени.

Получается, что как будто имеем дело с одной частицей, масса 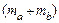которой сосредоточена в точке центра масс. Средняя энергия ее поступательного движения 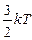такая же, что и для одной частицы. Тогда остальная энергия, 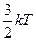, должна приходиться на внутренние степени свободы: две вращательные и одну колебательную.

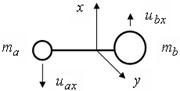
Пусть теперь в результате столкновения один из атомов молекулы получил импульс в направлении, перпендикулярном оси молекулы. В системе центра масс это приводит к появлению одинаковых по величине, но противоположно направленных импульсов у обоих атомов. Это означает вращение молекулы относительно оси y, как показано на рис. 4.2. Таким образом, в начальный момент времени атомы движутся вдоль оси х в противоположные стороны.

В системе центра масс скорости двух атомов в молекуле есть

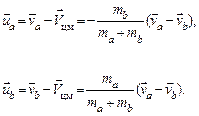(4.16)

(Отметим, что суммарный импульс 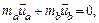как и должно быть при движении в системе центра масс).

Рис. 4.2.

в лабораторной системе координат для средних значений энергий обоих атомов сразу после столкновения из (1.23) следует, что

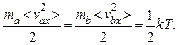(4.17)

В системе центра масс из (4.16) получим

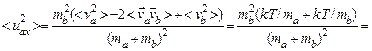
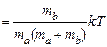(4.18)

(Скалярное произведение в числителе здесь тоже при усреднении даст нуль из-за независимости скоростей.) Аналогично получится, что

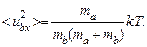(4.19)

Отсюда

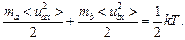(4.20)

Таким образом, средняя кинетическая энергия вращения равна 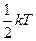. Вращение вокруг оси x должно дать такой же результат. По причинам, которые будут понятны из материала следующего раздела, вращение вокруг оси z (ось молекулы) отсутствует.

Для кинетической энергии колебаний вдоль оси молекулы аналогичное рассмотрение также дает 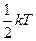. Столько же должен составить вклад средней потенциальной энергии колебаний (как известно, при колебаниях кинетическая и потенциальная энергии постоянно между собой обмениваются, средние их значения равны друг другу).

Отметим, что данные результаты можно получить и методом статсумм. Энергию вращения вокруг оси у можно представить через импульс р = m_au_ax = m_bu_bx атома а или b (они равны друг другу):

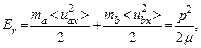(4.21)

где 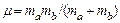есть приведенная масса. Импульс р может меняться от – ¥ до ¥. Тогда статсумма определяется как интеграл по всем возможным р:

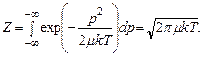(4.22)

Отсюда

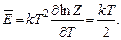
Для колебаний также можно получить аналогичный результат методом статсумм. Энергия осциллятора есть

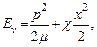
где χ - коэффициент жесткости связи в молекуле, х – величина смещения. Тогда статсумма определяется как интеграл по всем возможным р и х:

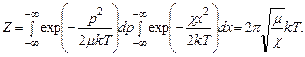(4.23)

Отсюда

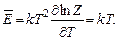
Вспомним, что у молекулы три поступательные степени свободы, на каждую из них приходится по 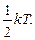В итоге получаем закон равнораспределения по энергиям: на каждую степень свободы в молекуле приходится средняя энергия, равная 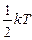(на колебательные степени - kТ).

В итоге для двухатомной молекулы средняя энергия оказывается равной 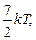или для моля двухатомного газа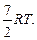

Дата добавления: 2014-01-07