Графический метод решения задач

Задача № 1.1.1.

f = – х 1 + 5 х 2 ¾> min;

4 х 1+ 3 х 2 £ 24,

х 1– 10 х 2 £ 0,

8 х 1– 3 х 2 ³ 0,

5 х 1+ 3 х 2 ³ 15,

х 1³0, х 2³ 0. (1)

Совокупность переменных хj, удовлетворяющих условию (1), называется областью допустимых решений. Допустимое решение, обращающее целевую функцию в min или max, называется оптимальным. Для его определения необходимо построить область допустимых решений (область определения). Так как в условии задачи заданы две переменные, то область допустимых решений находится на плоскости х 10 х 2. Каждое неравенство (1) определяет полуплоскость, а равенство – прямую. Для построения полуплоскости необходимо найти ее границу и установить, с какой стороны от нее лежит искомая полуплоскость. Перепишем условия (1) в виде равенств (2) и пронумеруем их.

4 х 1+ 3 х 2	=	24 (I),
х 1– 10 х 2	=	0 (II),
8 х 1– 3 х 2	=	0 (III),
5 х 1+ 3 х 2	=	15 (IV).	(2)

Введем систему координат х 10 х 2 и построим последовательно эти прямые – границы полуплоскостей. Для построения прямой на плоскости необходимо определить любые две точки, лежащие на этой прямой. Если прямая пересекает оси 0 х 1и 0 х 2, то можно найти координаты точек ее пересечения с осями координат. Определим координаты пересечения прямой (I) с осью 0 х 1: х 1=0; Þ 3 х 2= 24; Þ х 2= 8. Соответственно определим координаты второй точки пересечения первой прямой с осью 0 х 2: х 2=0; Þ 4 х 1= 24; Þ х 1= 6. Следовательно, точки пересечения прямой (I) с осями координат равны (0,8) и (6,0). Построим эту прямую (рис. 1).

Определим полуплоскость. Для этого подставим в первое неравенство (1) координаты любой точки, не лежащей на данной прямой, например (0,0). Тогда из первого условия следует: 4×0+3×0 £24, значит, неравенство справедливо, откуда следует, что полуплоскость лежит с той стороны прямой, где находится точка с координатами (0,0).

Рис. 1

Обозначим данную полуплоскость штриховыми линиями и укажем расположение ее относительно прямой стрелками (рис. 2).

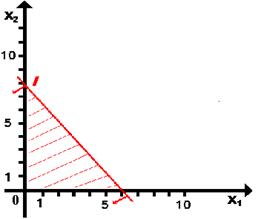Рис. 2

Аналогичным образом строятся и другие полуплоскости. Необходимо учесть, что прямые (II) и (III) проходят через начало координат, т.е. точку (0,0). Координаты второй точки желательно брать пропорционально коэффициентам в уравнении искомой прямой. Например, для второй прямой – точки (0,0) и (10,1), а для третьей – (0,0) и (3,8). После построения всех полуплоскостей область допустимых решений примет следующий вид (рис. 3):

Рис. 3

Область допустимых решений представлена в виде выпуклого многоугольника ABCD. Следующий этап в решении задачи – построение целевой функции:

f = – х 1+ 5 х 2 ¾> min.

Целевая функция f определяет на плоскости прямую, которая должна проходить через точку или сторону многоугольника и иметь наименьшее значение. Построим направляющий вектор для этой прямой. Данный вектор перпендикулярен искомой прямой, и его направление всегда определяет максимум целевой функции. Противоположное направление вектора определяет минимум. Обозначим этот вектор через . Он проходит через точку (0,0) и (–1,5). Координаты второй точки берут из коэффициентов целевой функции и с их помощью определяют направление вектора . Перпендикулярно ему построим прямую – х 1+ 5 х 2=0. Как было сказано выше, вектор всегда показывает направление возрастания значения целевой функции (max), противоположный ему вектор – – направление убывания значения целевой функции (min). Перемещаем прямую – х 1+5 х 2=0 по области определения параллельно самой себе в направлении min. Целевая функция f достигнет своего минимального значения в точке С (рис. 4).

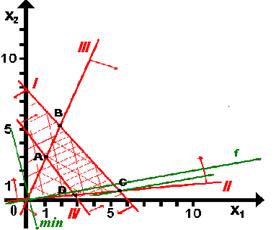Рис. 4

Оптимальному решению задачи (1) соответствует точка С, которая лежит на пересечении прямых (I) и (II):

4 х 1+ 3 х 2= 24;

х 1– 10 х 2= 0.

Для решения данной системы уравнений умножить второе уравнение на 4 и сложить соответственно по элементам с 1-м уравнением:

4 х 1+ 3 х 2 = 24;

4 х 1– 40 х 2 = 0.

Вычтем из первого уравнения второе, получим: 43х2= 24 Þ х 2= 0,56.

Подставив найденное значение х 2во второе уравнение, получим:

х 1= 10 х 2Þ х 1=5,6. Подставив координаты точки С в целевую функцию, получим следующий результат:

f min = – 5,6 + 5×0,56 = – 2,8.

Окончательный результат задачи запишем в следующем виде:

х 1= 5,6, х 2= 0,56; f min = – 2,8.

Решение данного примера на ПЭВМ осуществляется программным комплексом «Блок-3». С его помощью производятся ввод, решение и вывод результативной информации на внешний носитель. Простота и доступность комплекса позволит без труда освоить его и применять на практике.

Задача № 1.1.2.

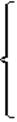f = 2 х 1+ 3 х 2 ¾> max;

2 х 1+ 3 х 2 £ 12,

2 х 1– 5 х 2 £ 0,

7 х 1– 2х2³ 0,

х 1, х 2³ 0. (3)

Определения и построение области допустимых решений аналогичны заданию 1.1.1. Окончательный вид области допустимых решений представлен на рис. 5 многоугольником АВС (точка А совпадает с точкой 0).

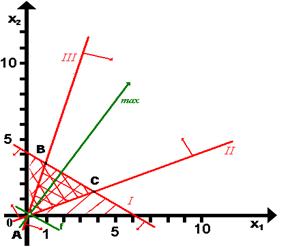
Рис. 5

Очевидно, что прямая, определяющая целевую функцию, совпадает с прямой, образующей сторону многоугольника ВС. Отсюда следует, что решением данной ЭММ являются точки, лежащие на стороне ВС много-

угольника АВС. Для записи решения ЭММ необходимо найти координату x 1 B – точки В и x 1 C – точки С. Определив их, мы сможем найти отрезок, лежащий на оси 0 x 1(рис. 6).

Рис. 6

Координаты точки В – x1 B определяются в результате пересечения прямых 2 х 1+ 3 х 2 = 12 и 7 х 1– 2 х 2 = 0. Для этого необходимо решить систему уравнений:

2 х 1+ 3 х 2= 12 ´ 2 Þ 4 х 1+ 6 х 2= 24;

7 х 1– 2 х 2= 0 ´ 3 Þ 21 х 1– 6х2= 0.

Сложив два последних уравнения, получим: 25 х 1=24, х 1=0,96. Из этого следует, что x 1 B =0,96. Координата точки С – x 1 C определяется в результате пересечения прямых 2 х 1+ 3 х 2=12 и 2 х 1–5 х 2=0. Решим систему уравнений:

2 х 1+ 3 х 2= 12 ´ 5 Þ 10 х 1+ 15 х 2= 60;

2 х 1– 5 х 2= 0 ´ 3 Þ 6 х 1 – 15 х 2= 0.

Сложив два последних уравнения, получим: 16 х 1= 60, х 1= 3,75, откуда следует, что x 1 C = 3,75.

Значение целевой функции для данной ЭММ равно 12 (так как уравнение прямой, на которой определен отрезок ВС – 2 х 1+3 х 2= 12).

Таким образом, ответ данной задачи:

x 1Î[ x 1 B; x 1 C ] Þ x 1Î[0,96; 3,75];

2 х 1+ 3 х 2=12 Þ 3 х 2= 12 – 2 х 1Þ х 2= (12 – 2 х 1)/3.

Полный ответ данного примера запишется в следующем виде:

x 1Î[0,96; 3,75]; x 2= (12 – 2 х 1)/3; f max = 12.

Задача № 1.1.3.

f = 2 х 1+ 3 х 2 ¾> max;

2 х 1+ 3 х 2 ³ 12,

2 х 1– 5 х 2 £ 0,

7 х 1– 2 х 2³ 0,

х 1, х 2 ³0. (4)

Используя схему построения области допустимых решений задач 1.1.1–1.1.2, получим следующий график (рис. 7):

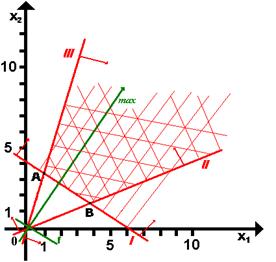Рис. 7

Из графика видно, что для данной ЭММ задачи ЛП оптимального решения нет, так как область допустимых решений в направлении целевой функции неограничена.

Ответ: нет оптимального решения.

Задача № 1.1.4.

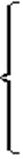f = 2 х 1+ 3 х 2 ¾> max;

х 1+ х2 £ 2,

2 х 1+ 3 х 2³ 12,

2 х 1– 5 х 2£ 0,

7 х 1– 2 х 2³ 0,

х 1, х 2³ 0. (5)

Используя график задачи 1.1.3 и достроив первую полуплоскость х 1+х2£ 2, получим область определения, показанную на рис. 8.

Рис. 8

Из графика (рис. 8) видно, что для данной ЭММ области допустимых решений нет. Ответ: нет области допустимых решений.

Задача № 1.1.5.

f = – х 1+ 5 х 2 ¾> min;

10 х 1+ 3 х 2£ 30,

10 х 1+ 5 х 2³ 50,

2 х 1– 6 х 2£ 0,

х 1, х 2³ 0. (6)

Область определения ЭММ (6) представлена на рис. 9. Из анализа графика следует, что областью допустимых решений будет являться точка А с координатами (0,10) (10 х 1+ 5 х 2= 50, х 1= 0, 5 х 2= 50, х 2=10). В случае, когда решением ЭММ является единственная точка, целевую функцию можно не строить.

Ответ: x 1= 0; x 2=10; fmin = 0+5×10 = 50.

Рис. 9

Таким образом, при решении задач ЭММ ЛП возможны следующие ситуации:

– задача имеет одно оптимальное решение;

– задача имеет бесконечное число оптимальных решений;

– задача не имеет оптимального решения;

– задача не имеет области допустимых решений.

На практике ЭММ ЛП не имеет решений только в том случае, если некорректна постановка задачи.

Как показывает опыт разработки ЭММ, основная сложность состоит в описании экономико-технологических процессов в модели и выборе критерия оптимизации. Отсюда следует, что необходимо точно определить нормативные параметры. Это в свою очередь требует поставленного учета и анализа на исследуемом объекте. В то же время особое значение в составлении модели приобретает уровень подготовки специалиста. От его умения выявить основные звенья технологического процесса, определить этапы решения задачи и сформулировать цели исследования будет зависеть и качество решения данной проблемы.

Задача № 1.1.6.

Предприятие может организовать производство своей продукции двумя способами. При первом способе предприятие за месяц выпускает C ₁ тыс. изделий, при втором – C ₂ тыс. изделий. Расход производственных, людских ресурсов, амортизация оборудования и ограничения ресурсов, приведены ниже в таблице.

Сколько месяцев должно работать предприятие, каким способом организовать производство, чтобы обеспечить максимальный выпуск продукции.

1) Решить графическим способом;

2) Решить на базе комплекса «Блок-3»;

3) Симплекс-методом.

Таблица 1

Дата добавления: 2014-01-07