III. Целевая функция

II. Ограничение

I. Переменные

Условия по затратам времени

Ограничение по ресурсам

Условия по затратам и выпуск продукции

№ варианта	Ограничения по ресурсам Табл. 2	Условия по затратам времени Табл. 3	Выпуск продукции
C 1	C 2
	1, 7	8, 15

Таблица 2

Производственный и людской ресурс	Расход ресурсов за 1 месяц	Ограничение по ресурсам
1 способ	2 способ
1. Сырье, т
7. Оборудование тыс. руб.

Таблица 3

на операции L ₁ (первом) и L ₂ (втором) способе производства

№	Условия производства
	6 L 1 – L 2 ≥ 0
	3 L 1 – 8 L 2 ≤ 0

Составим ЭММ: формализация задачи.

х ₁– 1-й способ, мес.;

х ₂– 2-й способ, мес.

1. Условие по затратам на сырье:

3 x ₁ + 2 x ₂ £ 6.

2. Условие по затратам на оборудование:

5 x ₁ + 2 x ₂ £ 10.

3. Условие 1-е по затратам времени на операции:

6 x ₁ – x ₂ ≥ 0.

4. Условие 2-е по затратам времени на операции:

3 x ₁ – 8 x ₂ £ 6.

Критерий ЭММ – максимум выпуска продукции, тыс. штук, при организации производства 1-м и 2-м способом.

7 x ₁ + 9 x ₂ ® max.

В результате формализации условий табл. 1, табл. 2 и табл. 3, ЭММ ЛП примет вид:

1) Построение на базе «Блокнот-4».

Используя правила построения (задания 1.1.1 и 1.1.2) выразим основные уравнения, необходимые для описания графика, причем необходимо х ₂ заменить y, х ₁ – х:

3 х ₁ + 2 х ₂ £ 6 Þ 3 х ₁ + 2 х ₂ = 6 Þ y =(6–3* x)/2

5 х ₁ + 2 х ₂ £ 10 Þ 5 х ₁ + 2 х ₂ = 10 Þ y =(10–5* x)/2

6 х ₁ – х ₂ ³ 0 Þ 6 х ₁ – х ₂ = 0 Þ y =6* x

3 х ₁ – 8 х ₂ £ 0 Þ 3 х ₁ – 8 х ₂ = 0 Þ y =(3* x)/8

7 х ₁+ 9 х ₂ = 0 Þ y = –(7* x)/9.

Найти точки пересечения графиков с осями координат. Из формул следует, что только первые два графика имеют точки пересечения с осями координат:

1-й график.

Пересечение с осью 0 y (значение x =0): y=(6–3*0)/2 Þ y =3.

Пересечение с осью 0 х (значение y =0): 0=(6–3* x)/2 Þ x =2.

2-й график.

Пересечение с осью 0 y (значение x =0): y=(10–5*0)/2 Þ y =5.

Пересечение с осью 0 х (значение y =0): 0=(10–5* x)/2 Þ x =2.

Для отображения всего графического решения, необходимо определить точку, соответствующую оптимальному решению. Очевидно, она является решением системы уравнений:

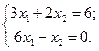(7)

Решения данной системы: х ₁=0,4 и х ₂ =2,4 Þ y =2,4 и х =0,4, следовательно,

Фрагмент исходной информации на листе Excel «Блокнота-4» имеет следующий вид:

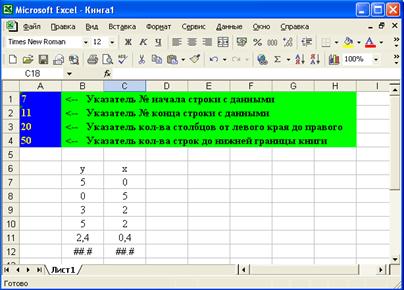
Рис. 10. Фрагмент исходной информации для построения графика

Фрагмент режима «Построение графика»:

Рис. 11. Вид записи графиков

Первоначальный вид графика представлен на рис. 12.

Рис. 12. Вид графиков в режиме «Блокнот-4»

Скопировав через буфер изображение в Paint, выполнив доработку, получим окончательный вид графика:

Рис. 13. График задания 1.1.6

2) Решение на базе комплекса «Блок-3».

Исходная информация в «Блок-3» представлена на рис. 14.

Рис. 14. Исходная информация ЭММ ЛП задания 1.1.6

В результате оптимизации, решение представлено на рис. 15.

Рис. 15. Решение ЭММ ЛП задания 1.1.6

Информация рис. 14 и рис. 15 взята с экрана дисплея ПЭВМ. Аналогичная информация представлена и на бумажном носителе.

3) Решение задачи Симплеск-методом.

Из графика рис.13 видно, что второе ограничение роли не играет. Для удобства решения, левую часть ограничения (III), перенесем в правую, получим:

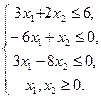
Приведем задачу к каноническому виду:

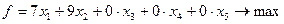
Составим первую симплексную таблицу:

ci	Базисные переменные						f (x)max
x 1	x 2	x 3	x 4	x 5	bi
	x 3
	x 4	–6
	x 5		–8
Индексная строка	–7	–9

Опорный план x *=(0,0,6,0,0). В индексной строке две отрицательных числа: –7 и –9, найденное решение не является оптимальным и его можно улучшить. Наибольшее число со знаком минус в индексной строке: –9, следовательно выбираем в качестве ключевого столбца базисной переменной х ₂. Для выбора ключевой строки, необходимо элементы столбца b_i разделить соответственно на элементы выбранного нами столбца х ₂, получим: (6/2; 0/1; 0/–8)=(3; 0; –0). Из трех полученных чисел необходимо выбрать положительный min элемент– он равен 0 и расположен на втором месте, следовательно, ключевой строкой является вторая строка. Выводим из базисной переменной переменную х ₄ (вторая ключевая строка) и заменяем ее на х ₂ и обнуляем простейшими операциями элементы, стоящие во втором столбцу (1-й и 3-й столбцы): вычесть из первой строки вторую, умноженную на 2; сложить вторую строку умноженную на 8 с третьей и соответственно с индексной строкой (умножить вторую строку на 9 и сложить с индексной строкой). Получим вторую симплекс таблицу:

ci	Базисные переменные						f (x)max
x 1	x 2	x 3	x 4	x 5	bi
	x 3				–2
	x 2	–6
	x 5	–45
Индексная строка	–61

Получено решение: x *=(0,0,6,0,0). В индексной строке имеется одна отрицательная переменная. Следовательно, полученное решение можно улучшить. Очевидно, что ключевой столбец 1-й, а строка 2-я, соответственно ввод базис переменную х ₁ а выводим переменную х ₃. Разделив первую строку на 15. Последовательно, взяв первую строку: умножить на 6 и сложить со второй строкой; умножить на 45 и сложить с третьей; умножив на 7 сложить с индексной строкой, в результате получим третью симплекс таблицу:

ci	Базисные переменные						f (x)max
x 1	x 2	x 3	x 4	x 5	bi
	x 1			1/15	–2/15		0,4
	x 2			6/15	–12/15		2,4
	x 5				–1
Индексная строка			61/15	13/15		24,4

Все числа в индексной строке положительны, следовательно, решение оптимальное: x *=(0,4; 2,4; 0; 0; 18), f _max=24,4.

Полученное решение гласит: первым способом организации производства, предприятия будет работать 0,4 месяца; вторым– 2,4 месяца, при этом общий объем продукции составит 24,4 тыс. изделий.

Дата добавления: 2014-01-07