Ограничения

Переменные

Стоимость 1 ц минерального удобрения тыс. руб.

№	Наименование минеральных удобрений	Стоимость
	N	3,5
	P	6,0
	K	5,0

Решение ЭММ ЛП выполняем согласно требованиям построения ЭММ ЛП.

Постановка задачи определена в ее условии.

Формализация задачи. Этот этап будет представлен тремя шагами:

1) переменные;

2) ограничения;

3) целевая функция.

В начале построения модели необходимо определить основные переменные (из постановки задачи) и оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум прибыли. Таким образом, становится ясно, что в качестве основных переменных будут посевы сельскохозяйственных культур. Необходимо подчеркнуть, что в обозначении переменных нужно указывать единицу измерения, чтобы не допустить ошибку при вводе ограничений. Определим эти переменные.

x ₁ – посевная площадь пшеницы озимой, га;

x ₂ – посевная площадь ячменя, га;

x ₃ – посевная площадь картофеля, га;

x ₄ – посевная площадь сахарной свеклы, га;

x ₅ – посевная площадь капусты, га.

Три переменные, обозначающие потребности в минеральных удобрениях, определим в конце ограничений.

Необходимо оставить 10–15 строчек для ввода переменных по мере построения структурной ЭММ. Переходим ко второму шагу построения ЭММ.

Определим основные виды ограничений для данной ЭММ:

1) Ограничение по пашне.

2) Введение севооборотов.

3) Введение ограничений по ресурсам: материально-денежным или человеческим.

4) Введение балансовых уравнений по каждой культуре.

5) Введение проводок для каждого балансового уравнения (условий поставок).

6) Расчет потребности в минеральных удобрений.

7) Определит стоимость товарной продукции исходя из балансовых уравнений каждой культуры.

8) Определить все затраты на производство с.-х. продукции

Согласно выше приведенным условиям, введем следующие ограничения:

– площадь пашни – 6 500 га;

– сумма посевных площадей пшеницы и ячменя больше суммы посевных площадей картофеля и сахарной свеклы (севооборот 1);

– посевная площадь капусты не более 30 % от всей посевной площади (севооборот 2);

– затраты на производство не должны превышать 110 000 чел /час.

Запишем эти ограничения.

Ограничение по пашне:

x ₁ + x ₂ + x ₃ + x ₄ + x ₅£ 6 500.

Принято записывать ограничения по следующему правилу:

1) в левой части записываются только переменные с коэффициентами;

2) индексы при переменных должны быть расположены в порядке возрастания;

3) в правой части записывать только объемы значений ограничений;

4) при вводе ограничений в ПЭВМ с помощью программного комплекса «Блок» знаки ³ и £ заменяются соответственно на знаки > и <;

5) если запись ограничения удовлетворяет требованиям 1–3, то необходимо заключить его в прямоугольник, что позволит быстро и без ошибок построить развернутую схему матрицы ЭММ.

Таким образом, ограничение 1 примет окончательный вид:

x ₁ + x ₂ + x ₃ + x ₄ + x ₅£ 6 500.

Условие по севообороту 1: x ₁+ x ₂ ³ x ₃+ x ₄.

Перенесем переменные из правой части в левую, получим окончательный вид ограничения:

x ₁+ x ₂– x ₃ – x ₄³0.

Условие по севообороту 2:

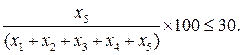
Разделив левую и правую часть на 100, перенести знаменатель левой части в правую, получим следующий вид ограничения:

x ₅£ 0,3(x ₁+ x ₂ + x ₃ + x ₄ + x ₅ ).

Раскроем скобки и перенесем переменные из правой части в левую часть. Получим окончательный вид ограничения:

– 0,3 x ₁ – 0,3 x ₂– 0,3 x ₃ – 0,3 x ₄+ 0,7 x ₅£0.

4. Ограничение по затратам труда:

20 x ₁ +16 x ₂ + 100 x ₃ + 280 x ₄ + 160 x ₅£ 110 000.

Так как значение объема ограничения превышает пятизначное число, целесообразно поделить данное условие на 1 000. В этом случае получим следующее ограничение:

0,02 x ₁+0,016 x ₂ + 0,1 x ₃ + 0,28 x ₄ + 0,16 x ₅£ 110.

Дальнейшее построение ЭММ зависит от целевой функции. В нашем примере критерий ЭММ – максимум прибыли. Значит, для ее определения необходимо найти выручку от товарной продукции и затраты на ее производство. Для определения товарной продукции надо составить балансовые уравнения по каждому ее виду, в левой части которых –поступление продукции, в правой – расход продукции. Левая часть представляет собой валовую продукцию плюс остаток продукции прошлого года. В условии задачи ничего не сказано об остатке. Поэтому будем считать его равным нулю. Тогда для записи левой части балансового уравнения необходимо ввести новую переменную x ₆ – валовая продукция озимой пшеницы или записать это выражение через произведение 1,7 x ₁. Воспользуемся вторым выражением.

Для записи правой расходной части балансового уравнения необходимо проанализировать условие задачи и определить «статьи» расхода продукции. Для каждого вида расхода вводим переменную. Тогда из условия задачи следует:

x ₆ – озимая пшеница на семена, т;

x ₇ – озимая пшеница в страховой фонд, т;

x ₈ – поставка озимой пшеницы на элеватор, т;

x ₉ – озимая пшеница на рынок, т.

При вводе переменных обратить внимание, что всегда последней переменной в балансовом уравнении будут поставки продукции на рынок, или, другими словами, реализация продукции по своему усмотрению.

После ввода переменных запишем балансовое уравнение по озимой пшенице:

5. Условие по балансу озимой пшеницы:

1,7 x 1= x 6+ x 7 + x 8+ x 9

Þ

1,7 x 1– x 6 – x 7 – x 8 – x 9= 0.

После ввода балансового уравнения необходимо произвести увязку переменных, если это возможно. Из приведенного уравнения видно, что ее можно провести по переменным x ₆и x ₇. Запишем эти ограничения.

6. Условие по семенному фонду озимой пшеницы:

x 6= 0,03×1,7 x 1

Þ

– 0,051 x 1+ x 6 = 0.

7. Условие по страховому фонду озимой пшеницы:

x 7= 0,06×1,7 x 1

Þ

– 0,102 x 1+ x 7 = 0.

8. Условие по поставке зерна озимой пшеницы на элеватор:

x 8 £ 0,15×1,7 x 1

Þ

– 0,255 x 1+ x 8 £ 0.

Поставки на рынок увяжутся уравнением по товарной продукции, которое мы введем после построения всех балансовых уравнений по сельскохозяйственным культурам.

Затем можно перейти к построению балансового уравнения по ячменю. Введем его левую часть, для чего необходимо определить валовой сбор данной культуры. В нашем случае он равен 1,9 x ₂. Введем переменные для правой части балансового уравнения:

x ₁₀ – ячмень на семена, т;

x ₁₁ – ячмень в страховой фонд, т;

x ₁₂ – поставка ячменя на элеватор, т;

x ₁₃ – ячмень на рынок, т.

9. Условие по балансу ячменя:

1,9 x 2= x 10 + x 11 + x 12 + x 13

Þ

1,9 x 2– x 10– x 11– x 12– x 13= 0.

10. Условие по семенному фонду ячменя:

x 10= 0,03×1,9 x 2

Þ

– 0,057 x 2+ x 10=0.

11. Условие по страховому фонду ячменя:

x 11= 0,06×1,9 x 2

Þ

– 0,114 x 2+ x 11=0.

12. Условие по поставке зерна ячменя на элеватор

x 12= 0,15×1,9 x 2

Þ

– 0,285 x 2+ x 12=0.

Перейдем к построению условий для картофеля. Валовой сбор картофеля равен 9,5 x ₃. Для правой части балансового уравнения введем следующие переменные:

x ₁₄ – поставки картофеля в магазин, т;

x ₁₅ – картофель в страховой фонд, т;

x ₁₆ – картофель на рынок, т.

13. Условие по балансу картофеля:

9,5 x 3 = x 14 + x 15 + x 16

Þ

9,5 x 3 – x 14 – x 15 – x 16= 0.

14. Условие поставки картофеля в магазин:

x 14

³

50.

Условие по страховому фонду картофеля:

x 15 = 0,25×9,5 x 3

Þ

–2,375 x 3 + x 15= 0.

После ввода увязок по расходной части балансового уравнения перейдем к построению балансового уравнения для сахарной свеклы.

Определим его левую часть. Валовой сбор сахарной свеклы будет равен 17,8 x ₄. Для определения правой части введем следующие переменные:

x ₁₇ – поставки сахарной свеклы на переработку, т;

x ₁₈ – сахарная свекла на рынок, т;

16. Условие по балансу сахарной свеклы:

17,8 x 4 = x 17 + x 18

Þ

17,8 x 4 – x 17 – x 18= 0.

17. Условие поставки сахарной свеклы на переработку:

x 17

³

70.

Перейдем к вводу ограничений для капусты. Левая часть балансового уравнения равна 28 x ₅. Определим дополнительные переменные по этой культуре для правой части:

x ₁₉ – закладка капусты в овощехранилище, т;

x ₂₀ – поставка капусты для собственных нужд, т;

x ₂₁ – капуста на рынок, т.

18. Условие по балансу капусты:

28 x 5 = x 19 + x 20+ x 21

Þ

28 x 5 – x 19 – x 20– x 21= 0.

19. Условие поставки капусты в овощехранилище:

x ₁₉£65.

20. Условие поставки капусты на собственные нужды:

x 20 = 0,3×28 x 5

Þ

–8,4 x 5 + x 20= 0.

Последним ограничением ЭММ заканчиваем рассмотрение балансовых уравнений. Теперь приступим к определению основных элементов по минеральным удобрениям:

x ₂₂ – N, ц;

x ₂₃ – P, ц;

x ₂₄ – K, ц.

21. Расчет потребности в N:

x ₂₂ = 0,16 x ₁ + 0,17 x ₂ + 0,31 x ₃ + 0,24 x ₄ + 0,09 x ₅,

или в окончательной форме записи:

0,16 x ₁ + 0,17 x ₂ + 0,31 x ₃ + 0,24 x ₄ + 0,09 x ₅ – x ₂₂ = 0.

22. Расчет потребности в P:

x ₂₃ =0,2 x ₁ + 0,26 x ₂ + 0,23 x ₃ + 0,44 x ₄ + 0,21 x ₅,

или в окончательной форме записи:

0,2 x ₁ + 0,26 x ₂ + 0,23 x ₃ + 0,44 x ₄ + 0,21 x ₅ – x ₂₃ = 0.

23. Расчет потребности в K:

0,24 x ₁ + 0,33 x ₂ + 0,26 x ₃ + 0,56 x ₄ + 0,17 x ₅ – x ₂₄ = 0.

Введем оставшиеся две переменные для целевой функции:

x ₂₅ – общие затраты на производство, тыс. руб.

Произведем увязку этих переменных.

24. Условие по затратам на производство продукции:

x ₂₅ = 0,25 x ₁+0,3 x ₂+1,4 x ₃ + 0,6 x ₄ +1,9 x ₅ + 3,5 x ₂₂ + 6,0 x ₂₃ +5,0 x ₂₄.

Перенесем переменную x ₂₆ в правую часть условия и получим следующий вид ограничения:

0,25 x ₁+ 0,3 x ₂ +1,4 x ₃ + 0,6 x ₄ + 1,9 x ₅ + 3,5 x ₂₂+6,0 x ₂₃ +5,0 x ₂₄– x ₂₅= 0.

Дата добавления: 2014-01-07