Правило фаз Гиббса

Пусть имеется система, состоящая из трех фаз (I), (II), (III). Тогда условия равновесия можно записать следующим образом:

1) р⁽¹⁾ = р⁽¹¹⁾ = р⁽¹¹¹⁾ – условие механического равновесия,

2) Т⁽¹⁾ = Т⁽¹¹⁾ = Т⁽¹¹¹⁾ – условие термического равновесия,

m_i⁽¹⁾ = m_i⁽¹¹⁾ = m_i⁽¹¹¹⁾ – условие химического равновесия.

Из анализа этих условий и было получено правило фаз Гиббса, которое обычно формулируют следующим образом:

Число степеней свободы (f) равновесной термодинамической системы, на которую влияют только температура (Т) и давление (р), равно числу независимых компонентов системы (k) минус число фаз (Ф) плюс 2.

Математически правило фаз Гиббса записывается так: f = k – Ф + 2.

Число степеней свободы – это число независимых переменных, которые можно изменять произвольно в некоторых пределах так, чтобы число и природа фаз остались прежними.

Число степеней свободы характеризует вариантность системы, которая в зависимости от величины f может быть следующей:

1) нонвариантная система (безвариантная, f = 0),

2) моновариантная система (одновариантная, f = 1),

3) бивариантная система (двухвариантная, f = 2) и т.д.

На практике часто рассматривают влияние только одного переменного внешнего параметра на систему (т.е. берут или постоянное давление (тогда Т¹const), или постоянную температуру (тогда p¹const)). В этом случае n=1 и правило фаз Гиббса имеет вид:

f = k – Ф + 1. (единица относится к переменному внешнему параметру).

Пример 4.3 Определить число компонентов в системах:

a) Н₂(г) + I₂(г) = 2НI(г),

б) СaCO₃(тв) = СaO(тв) + СO₂(г).

Решение. a) В этой системе имеется одно уравнение, связывающее концентрации состовляющих частей:

H₂(г) + I₂(г) = 2HI(г)

,

следовательно, число компонентов в этой системе равно: .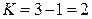

б) В этой системе также имеется только одно уравнение:

CaCO₃(тв) → СaO(тв) + СO₂(г)

,

следовательно, система будет двухкомпонентной, поскольку

.

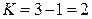4.3 Уравнение Клапейрона–Клаузиуса

Ограничимся рассмотрением фазовых переходов первого рода, для которых характерно равенство изобарно-изотермических потенциалов двух фаз и скачкообразное изменение энтропии S и объёма V.

Будем рассматривать равновесие чистого вещества в двух фазах однокомпонентной системы (k = 1). Это могут быть следующие процессы:

а) А_тв 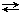А_ж – это процесс плавления (обратный процесс – кристаллизация);

б) А_ж А_газ – процесс испарения (обратный процесс – конденсация);

в) А_тв 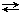А_газ – процесс сублимации (возгонки), (обратный процесс – десублимация или конденсация);

г) А_тв,a 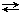А_тв,b – переход твердого тела из одной полиморфной (аллотропной) модификации в другую.

Для равновесия двух фаз (1) и (2) чистого вещества должны выполняться следующие условия:

р⁽¹⁾ = р⁽²⁾; (1)

Т⁽¹⁾ = Т⁽²⁾; (2)

m⁽¹⁾ = m⁽²⁾; (3)

Из соотношения (3)получим, что dm⁽¹⁾ = dm⁽²⁾ (4)

Но для чистого вещества химический потенциал m есть ни что иное, как молярная энергия Гиббса: .

Поэтому .

Но .

Для двух фаз (1) и (2) соотношение (4) примет вид:

(5)

Перегруппируем члены:

, откуда

.

Таким образом, получаем:

(6)

Соотношения (6) – это одна из форм записи уравнения Клапейрона-Клаузиуса.

Здесь DS_ф.п. – молярная энтропия фазового перехода (т.е. разность молярных энтропий вещества в двух фазах);

DV_ф.п. – разность молярных объемов вещества в двух фазах.

Если рассматривать обратимые изотермические фазовые переходы, то для них

.

Тогда уравнения (6) можно переписать в следующем виде:

(7)

Соотношение (7) – это тоже уравнение Клапейрона–Клаузиуса. Здесь Т – температура фазового перехода, DН_ф.п. – молярная теплота (энтальпия)

фазового перехода. Величину часто называют температурным коэффициентом давления насыщенного пара. Величина является угловым коэффициентом соответствующих кривых р = р(Т) (сублимации, испарения, плавления и полиморфных превращений).

Рассмотрим вначале равновесия с участием пара.

а) твердое вещество 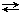пар – возгонка (сублимация);

б) жидкость 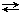пар – испарение (конденсация).

Если рассматривать равновесия в области температур, далеких от критической, то можно записать:

;

,

поскольку объемом конденсированной фазы по сравнению с объемом пара можно пренебречь. Считая, что пар подчиняется законам идеальных газов

для 1 моль газа имеем:

и ,

тогда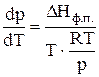

откуда следует, что (8)

Соотношение (8)–дифференциальная форма уравнения Клапейрона-Клаузиуса для процессов возгонки или испарения.

Так как DH_возг > 0 и DH_исп > 0, то lnp (а, значит, и р) – возрастающая функция, т.е. давление насыщенного пара над веществом увеличивается при увеличении температуры.

Разделим переменные в соотношении (8) Считаем, что в узком температурном интервале DH_ф.п. = const.

1) Возьмем неопределенный интеграл:

Отсюда:

или (9)

Уравнение прямой в координатах ln p-1/Т.

DН_возг > DН_испар,

Поэтому кривая возгонки р = р(Т) должна идти круче, чем кривая испарения. Если на одном графике изобразить зависимости в координатах lnp=f (), то будет наблюдаться следующая картина:

Линия АВ - соответствует процессу испарения, а линия ВС - процессу возгонки.

2) Возьмем определенный интеграл:

(10)

Рассмотрим теперь процесс плавления:

Воспользуемся уравнением Клапейрона-Клаузиуса в виде:

(11)

Здесь Т – температура плавления;

; DН_плавл – молярная теплота плавления.

Знак производной зависит от знака DV_плавл. Обычно _, поэтому

DV_плавл > 0. Есть несколько исключений (например, вода, висмут, галлий для которых DV_плавл < 0).

Температура фазового перехода между конденсированными фазами слабо зависит от давления р, поэтому соотношение (11) можно переписать в виде:

Пример 4.4 Как изменится температура плавления льда с изменением внешнего давления, если Δ_пл Н = 79,7 кал/г при t = 0 ^оС, а удельные объемы воды и льда при этой температуре равны соответственно: V _ж = 1,0001 см³/г и V _лед = 1,0908 см³/г.

Решение. Воспользуемся уравнением Клаузиуса – Клапейрона в виде (4.16)

.

,

.

Пример 4.5 Как изменится температура кипения воды с ростом давления, если при температуре t = 100 ^оС Δ_исп Н = 539,7 кал/г, V _пар = 1651 см³/г, V _ж = 1 см³/г.

Дата добавления: 2014-01-07