Эквивалентная электропроводность растворов электролитов

Хотя для понимания свойств электролитов удельная электропроводность представляет собой малоудобную величину, зато ее можно измерить непосредственно и затем пересчитать в эквивалентную электропроводность λ.

Эквивалентная электропроводность представляет собой электропроводность такого объёма раствора V (см³), который содержит 1 моль-экв растворенного вещества и заключён между двумя параллельными электродами соответствующей площади, находящихся на расстоянии в 1 см друг от друга:

Электропроводность электролита объема V складывается из суммы удельных электропроводностей æ_i, которые соответствуют каждому отдельному единичному объему. Таких единичных объемов будет V, следовательно

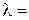æ V, т.к. 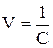, 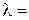æ / C, (12)

где С – концентрация раствора (моль-экв/см³).

Единица измерения удельной электропроводности 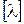– Ом^-1·см²·(моль-экв)^-1.

Или

,

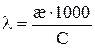если

.

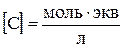Электропроводность с ростом температуры увеличивается, это в основном связано в основном с увеличением подвижности ионов. Обычно при повышении температуры на 1 К электропроводность увеличивается на 1,5 – 2%.

Эквивалентная электропроводность растворов электролитов с разбавлением возрастает и в области предельных разбавлений достигает предельного значения λ^∞, называемой электропроводностью при бесконечном разбавлении или предельной электропроводностью ( λ^∞).

Предельная электропроводность λ^∞ соответствует электропроводности бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.

Из уравнений (11) и (12) следует, что

. (13)

Произведение числа Фарадея на абсолютную скорость движения иона называют подвижностью иона:

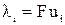. (14)

тогда

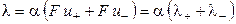, (15)

где λ₊ и λ_‑ ‑ подвижности катиона и аниона соответственно.

Подвижности ионов измеряются в тех же единицах, что и эквивалентная электропроводность (см²·Oм^-1·моль-экв^-1).

При бесконечном разведении (α = 1) и из выражения (15) получаем

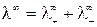, (16)

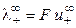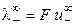где и ‑ предельные подвижности ионов.

Величина предельной эквивалентной электропроводности бесконечно разбавленного раствора электролита представляет собой сумму двух независимых слагаемых, каждое из которых соответствует определенному виду ионов. Это соотношение установлено Кольраушем и называется законом независимого движения ионов (законом Кольрауша):

Эквивалентная электропроводность при бесконечном разведении равна сумме предельных подвижностей ионов.

Сущность этого закона состоит в следующем: в предельно разбавленном растворе электролита катионы и анионы переносят ток независимо друг от друга.

Для сильных электролитов, диссоциирующих полностью, рассчитывают
коэффициент электропроводности:

,

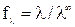который учитывает влияние электростатического взаимодействия ионов на скорость их движения.

Для связи электролитов рассчитывают степень диссоциации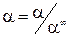

С учётом нового понятия ‑ подвижность иона ‑ для удельной электропроводности можно записать:

æ ,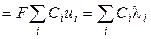

æ .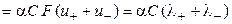

Отметим, что в современной научной и учебной литературе используется также понятие молярной электропроводности λ _m, которую легко связать с величиной λ, зная количество моль-эквивалентов (Z) в 1 моле вещества:

.

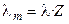Экспериментально было установлено, что для сильных электролитов зависимость эквивалентной электропроводности от 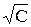– имеет прямолинейный характер (рис. 2) и выражается уравнением

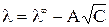, где

A – постоянная, зависящая от диэлектрической проницаемости и температуры. Экстраполяция значений 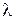к 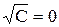позволит экспериментально определить 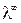сильных электролитов. Эти значения приведены в таблицах.

У ионов ОН ^‑ и ионов гидроксония наблюдается аномально высокие подвижности: при 25 ⁰С

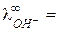198 и 350 (Ом^-1 моль-экв^-1 см²) (например 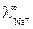= 50,1 Ом^-1 моль-экв^-1 см²), что объясняется особым – эстафетным механизмом их перемещения (рис. 3).

8.3 Зависимость удельной и эквивалентной электропроводностей от от концентрации для слабых и сильных электролитов.

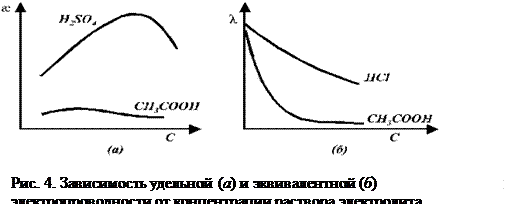
Кривые зависимостей 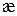от концентраций имеют максимум (рис.4а.). Концентрационную зависимость удельной электропроводности 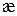слабых и сильных электролитов определяют два фактора. Для сильных электролитов – это концентрация раствора и подвижность ионов. С увеличением концентрации 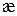увеличивается, а подвижность ионов уменьшается. При небольших концентрациях растворов электролитов превалирующим является первый фактор – концентрация, что приводит к росту 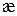с ростом С. В более концентрированных растворах, главным фактором становиться подвижность ионов, которая уменьшается с концентрацией и значения удельной электропроводности так же снижаются.

Для слабых электролитов на концентрационную зависимость 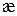так же влияют два фактора: концентрация (С) и степень диссоциации (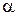). Для разбавленных растворов, так же как и для сильных электролитов, главным фактором в этом случае, является концентрация и с увеличением значений С удельная электропроводность увеличивается. Для концентрированных растворов, основным фактором уже становится влияние степени диссоциации (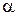), и так как с увеличением концентрации (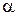) уменьшается (рис.4а), то уменьшается и удельная электропроводность.

Эквивалентная электропроводность слабых и сильных электролитов увеличивается с разбавлением (рис. 4 б). Для слабых электролитов это обусловлено в основном тем, что с увеличением разведения степень диссоциации электролита возрастает и в пределе стремится к 1. Рост эквивалентной электропроводности сильных электролитов связан в основном с увеличением подвижностей ионов. В области сильно разбавленных растворов подвижности ионов достигают своего предельного значения.

С позиций теории Дебая-Гюккеля уменьшение подвижности ионов с ростом концентрации обусловлено двумя эффектами торможения движения ионов за счёт электростатического взаимодействия между ионом и ионной атмосферой (рис.5,6.)

1) Эффект электрофоретического торможения обусловлен торможением движения центрального иона встречным движением ионной атмосферы и имеет гидродинамическую природу. Поскольку ионы гидратированы, то движение центрального иона происходит не в неподвижной среде, а в среде, перемещающейся ему навстречу. Движущийся ион находится под влиянием дополнительной тормозящей силы (силы электрофоретического торможения), что приводит к снижению скорости его движения. (рис.5.)

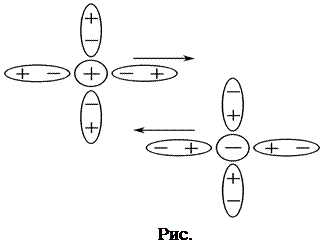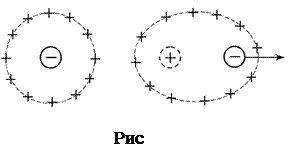2) Эффект релаксационного торможения. Ионная атмосфера обладает сферической симметрией до тех пор, пока отсутствует внешнее электрическое поле. Как только центральный ион начинает движение под действием электрического поля, симметрия ионной атмосферы нарушается. Перемещение иона сопровождается разрушением ионной атмосферы в одном положении иона и формированием ее в другом, новом. Этот процесс происходит с конечной скоростью в течение некоторого времени, называемого временем релаксации. В результате ионная атмосфера теряет центральную симметрию и позади движущегося иона всегда будет находиться некоторый избыток заряда противоположного знака, что и вызывает уменьшение его скорости движения. (рис.6.)

И только теория Дебая-Гюкеля-Онзагера позволила количественно учесть влияние этих эффектов на величину эквивалентной электропроводности раствора электролита. Теоретически было получено уравнение

,

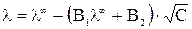в котором постоянные (В ₁·λ^∞) и В ₂ характеризуют влияние релаксационного и электрофоретического эффектов соответственно. Если концентрация в растворе стремиться к нулю С → 0 эти эффекты практически не проявляются и .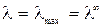

8.4 Экспериментальные приложения метода измерения электропроводности.

1. Определение константы диссоциации и степени диссоциации

слабых электролитов.

Степень диссоциации a слабого электролита может быть найдена из соотношения:

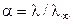. (17)

Константа диссоциации К_Д бинарного слабого электролита типа АВ связана со степенью диссоциации a уравнением

.

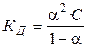С учетом (17), получаем

.

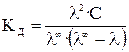Величина λ^∞ рассчитывается по закону Кольрауша (уравнение (16)).

2 Определение произведения растворимости

труднорастворимых соединений.

Растворимостью электролита (S) называется его концентрация в насыщенном растворе (моль/л), а произведением растворимости (ПР) – произведение активностей катиона и аниона труднорастворимой соли.

Насыщенный раствор труднорастворимой соли является очень разбавленным раствором (α → 1 и λ → λ^∞). Тогда для такого раствора можно считать, что эквивалентная электропроводность численно равна λ^∞.

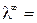( æ 1000) / C, где

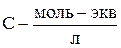
Найдя значение λ^∞ по табличным данным, и измерив удельную электропроводность раствора, можно вычислить концентрацию насыщенного раствора (в моль-экв/л),

C = ( æ ·1000) / λ^∞,

Затем перейдя от нормальной концентрации С к молярной концентрации С_M можно вычислить растворимость (S) соли.

Поскольку удельная электропроводность растворов труднорастворимых веществ (æ_р-ра) часто соизмерима с электропроводностью растворителя (воды) (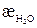), то она определяется из выражения:

,

где æ –удельная электропроводность соли

Для труднорастворимых солей активности катиона и аниона практически совпадают с их концентрациями, 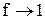поэтому

ПР =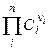

где n_i – стехиометрический коэффициент иона в уравнении диссоциации;

n – число видов ионов, на которые диссоциирует электролит;

C_i – концентрация иона, связанная с молярной концентрацией электролита С_М соотношением .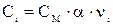

Так как a = 1, то 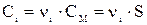, и произведение растворимости будет: .

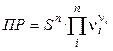Так, для труднорастворимого (бинарного) одно–одновалентного электролита, диссоцииирующего по схеме

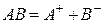, получим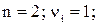 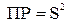(моль/л)².

Дата добавления: 2014-01-07