Миграция и диффузия

Миграция представляет собой передвижение ионов (или других заряженных частиц) под действием градиента электрического поля dU / dx, возникающего в электролите при прохождении тока через электрохимическую систему. Явление миграции лежит в основе электропроводности электролитов.

Различают удельную, эквивалентную и мольную электропроводность электролитов.

Электропроводность К - величина, обратная электрическому сопротивлению R. Так как

R = r 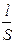, то К = 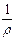× 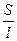= k ,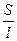

где r - удельное электрическое сопротивление; l - расстояние между электродами; S - площадь электрода; k - удельная электропроводность.

Удельная электропроводность k жидкости - это электропроводность одного кубического сантиметра раствора, заполняющего пространство между плоскими электродами одинаковой, очень большой площади, находящимися на расстоянии 1 см. Кубический сантиметр раствора должен находиться вдали от границ электрода. [k] = Ом^–1× см^–1.

Физический смысл k: по закону Ома R = U/I, K = I/U; I = i × S (i - плотность тока, или ток, приходящийся на 1 см² поверхности электрода; S - площадь электрода); U = E × l (Е - напряженность поля, или падение напряжения на 1 см расстояния; l - расстояние между электродами). Тогда

k 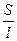= 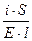; i = k× E.

При Е = 1 В/см i = k.

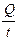I = ; i = .

Таким образом, k - это количество электричества, которое проходит в единицу времени через единицу поперечного сечения проводника при напряженности электрического поля 1 В/см.

Кривая зависимости удельной электропроводности растворов от концентрации обычно имеет максимум, четко выраженный для сильных электролитов и сглаженный для слабых.

Удельная электропроводность зависит от температуры. Зависимость дается эмпирическим уравнением

k_t = k₁₈ × [1 + a (t – 18)],

где a - температурный коэффициент электропроводности (a > 0); k₁₈ (k₂₅) - стандартное значение. Коэффициент a зависит от природы электролита; он равен для сильных кислот 0,0164, для сильных щелочей 0,0190, для солей 0,0220. В случае слабых электролитов a больше, чем для сильных. Следует отметить, что температурные коэффициенты электропроводности водных растворов и вязкости воды близки по своей величине, но обратны по знаку. Это свидетельствует о том, что увеличение удельной электропроводности с ростом температуры связано, главным образом, с уменьшением вязкости раствора.

Эквивалентная электропроводность l [в см²/(г-экв×Ом)] - это электропроводность такого объема (j см³) раствора, в котором содержится 1 г-экв растворенного вещества; раствор заполняет пространство между плоскими электродами одинаковой, очень большой площади, находящимися на расстоянии 1 см. Величина j, равная 1000/с см³/г-экв, называется разведением.

l = k× j; l = .

Мольная электропроводность электролита m - это произведение эквивалентной электропроводности на число грамм-эквивалентов в 1 моль диссоциирующего вещества.

Зависимость эквивалентной электропроводности от концентрации: для сильных электролитов в области малых концентраций соблюдается медленное линейное уменьшение l с увеличением , что соответствует эмпирической формуле Кольрауша (закону квадратного корня):

l = l_¥ - А,

где l_¥ - предельная эквивалентная электропроводность при бесконечном разведении: с ® 0, j ® ¥. А – эмпирическая постоянная. При несколько более высоких концентрациях сильных электролитов лучшее согласие с опытом дает уравнение, известное под названием закона кубического корня:

l = l_¥ - А.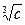

Для разбавленных растворов слабых электролитов вышеприведенные законы не соблюдаются.

Влияние природы растворителя на электропроводность: электропроводность растворов электролитов зависит, в первую очередь, от природы электролита и растворителя. Основными свойствами растворителя, обусловливающими характер изменения электропроводности, являются его вязкость и диэлектрическая проницаемость.

Повышение вязкости снижает электропроводность. Количественное выражение этого эффекта дается правилом Вальдена – Писаржевского:

l_оh_о = const,

l_о – мольная электропроводность электролита, экстраполированная до нулевой концентрации; h_о – вязкость чистого растворителя. Правило Вальдена – Писаржевского приближенно и оправдывается лишь для растворителей с близкими величинами диэлектрических проницаемостей.

Скорости движения катиона u¢ и аниона v¢ (см/с) зависят от природы ионов, напряженности электрического поля U/ l, концентрации, Т, вязкости среды и т.п. Скорость ионов пропорциональна приложенной силе, то есть напряженности поля

u¢ = u , v¢ = v ,

где u, v - скорости ионов в стандартных условиях, при напряженности поля, равной 1 В/см; они называются абсолютными подвижностями ионов и измеряются в см²/(с×В).

u×F и v×F - это скорости движения ионов, выраженные в электростатических единицах; они называются ионными электропроводностями (или просто подвижностями ионов):

u×F = l₊, v×F = l_–.

Для сильных электролитов l = l₊ + l_–,

для слабых l = (l₊ + l_–)×a.

При бесконечном разведении (j ® ¥, a ® 1)

l_¥ = l^о₊ + l^о_–

как для сильных, так и для слабых электролитов. Величины l^о₊ и l^о_– являются предельными электропроводностями (предельными подвижностями) ионов. Они равны эквивалентным электропроводностям катиона и аниона при бесконечном разведении и измеряются в тех же единицах, что и l и l_¥, то есть в см²/(Ом×г-экв). Вышеприведенное уравнение является выражением закона Кольрауша: эквивалентная электропроводность при бесконечном разведении равна сумме предельных подвижностей ионов.

Для всех электролитов можно записать

l_с = a_с ×l_¥, a_с = l_с / l_¥.

l₊ и l_– зависят от концентрации (разведения), особенно для сильных электролитов; l^о₊ и l^о_– - табличные величины.

Влияние природы иона (его радиуса и заряда) на величину подвижности иона отражено в формуле Стокса

u = ,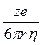

где е - заряд электрона; z - число элементарных зарядов иона; r - эффективный радиус иона (радиус гидратированного иона); h - коэффициент вязкости.

Уменьшение подвижности ионов и эквивалентной электропроводности lсильных электролитов с увеличением концентрации объясняется, по теории Дебая и Гюккеля, наличием ионной атмосферы. Из-за наличия ионной атмосферы при движении иона возникают два тормозящих эффекта: электрофоретический, обусловленный движением ионной атмосферы в сторону, противоположную направлению движения иона, и эффект релаксации, обусловленный асимметрией ионной атмосферы.

Онзагер вывел теоретическое уравнение, которое количественно связывает эквивалентную электропроводность с концентрацией и позволяет вычислить электрофоретический и релаксационный эффекты. Уравнение Онзагера имеет следующий вид:

l_с = l_¥ – (a + b l_¥),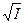

где первое слагаемое в скобках характеризует электрофоретический эффект, второе слагаемое характеризует эффект релаксации; a и b зависят от заряда ионов, Т, диэлектрической проницаемости растворителя D и вязкости растворителя h. Для 1-1 валентного электролита

l_с 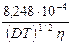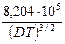= l_¥ – [ + l_¥].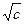

По виду уравнение совпадает с эмпирическим законом квадратного корня Кольрауша. Оно позволяют теоретически предсказать численное значение константы А уравнения Кольрауша. Формула Онзагера согласуется с опытными данными в той области концентраций, где приложим закон квадратного корня. При увеличении концентрации сходимость с опытом уменьшается.

Числом переноса ионов называется доля прошедшего через электролит электричества, перенесенная данным родом ионов:

t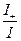₊ = , t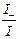_– = , t₊ + t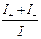_– = = 1;

I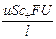₊ = , I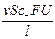_– = , I = I₊ + I_– = ;

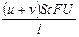t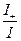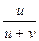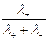₊ = = = , t_– = = = .

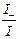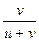Таким образом, число переноса равно отношению скорости движения (или подвижности) данного иона к сумме скоростей движения (или подвижностей) катиона и аниона. Так как подвижности катиона и аниона изменяются с концентрацией и температурой в общем случае неодинаково, то и числа переноса зависят от концентрации и температуры, хотя эта зависимость более слабая. Приведенные соотношения позволяют вычислить числа переноса, если известны значения подвижностей ионов. С другой стороны, опытное определение чисел переноса дает возможность вычислить подвижности.

Экспериментально числа переноса определяются по изменению концентрации ионов у электродов (метод Гитторфа):

= = .

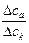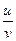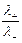Числа переноса определяются из соотношений

t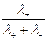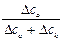₊ = = , t_– = = ,

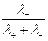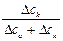где Dс_к – убыль электролита у катода, а Dс_а – убыль электролита у анода в ходе электролиза.

Определенные по методу Гитторфа числа переноса называются кажущимися числами переноса; они не являются истинными, так как этот метод не учитывает сольватации ионов. Измеряемые в методе Гитторфа концентрации определяются не только количеством катионов и анионов, но и количеством растворителя, перенесенного этими ионами в виде сольватных оболочек. Оболочки ионов разных знаков неодинаковы по величине.

Молекулярная диффузия представляет собой перемещение частиц под действием градиента химического потенциала d m/ dx, или приближенно – градиента концентрации dc/dx, возникающего в растворе в результате его качественной или количественной неоднородности. Молекулярная диффузия описывается законами Фика. Первый закон Фика описывает стационарную диффузию незаряженных частиц:

d n_i = – D _i S d t,

где n_i – число частиц, диффундирующих через поперечное сечение S; c_i – концентрация частиц; D _i – коэффициент диффузии – число i -х частиц, диффундирующих за единицу времени через единичное сечение, размерность коэффициента диффузии – м²/с.

D _i = ,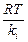

где k_i – коэффициент трения, откуда получаем, при использовании закона Стокса, уравнение Эйнштейна – Смолуховского:

D _i = ,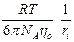

где r_i – радиус диффундирующей частицы (иона).

В соответствии с гидродинамической теорией электропроводности,

v_i = 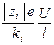, u_i = = ,

l _i = u_i F = = ,

где v_i – скорость движения иона (см/с); u_i – абсолютная подвижность иона; l _i – подвижность иона (ионная электропроводность).

Связь между подвижностью ионов и их коэффициентами диффузии устанавливается уравнением Нернста – Эйнштейна:

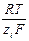D _i = u_i,

аналогичное уравнение передает зависимость между ионными электропроводностями и коэффициентами диффузии:

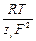D _i = l _i.

Оба уравнения относятся к бесконечно разбавленным растворам.

Диффузионный потенциал на границе двух жидких растворов для практически наиболее важных простых частных случаев можно рассчитать по следующим формулам (по методам Планка и Гендерсона):

1. Растворы одного и того же электролита МА, но разной концентрации:

y_D = – ln .

Если вместо концентраций подставить активности, то это уравнение можно применить и для концентрированных растворов

y_D = – ln ,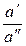

где подвижности ионов l_– и l₊ должны соответствовать их активностям в растворах I и II.

2. Растворы двух различных электролитов с одним общим ионом (например, типа М¢А и М¢¢А), причем концентрации электролитов одинаковы:

y_D = ln = ln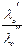

(учитывая, что l₊^о + l_–^о = l_о ).

Дата добавления: 2014-01-07