Пример 9

Решить дифференциальное уравнение:

(55)

Решение. Уравнение (55) представляет собой дифференциальное уравнение 3-го порядка, в котором в явном виде отсутствует искомая функция у. Следовательно оно является уравнением вида (53). Так как у^// - это низшая производная, входящая в уравнение (55), то мы можем понизить его порядок сразу на две единицы с помощью замены: у^|| = z (x). Тогда у^/// = z^/ (x) и уравнение (55) принимает вид:

(56)

Последнее уравнение есть уравнение 1-го порядка с разделяющимися переменными. Решим его (см § 3): ;

;

.

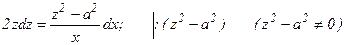
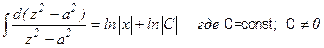
Положим С₁ = ± С (где C₁ = const, C₁ ≠ 0), тогда

,

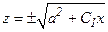но так как z = y^//, после обратной замены получаем следующее дифференциальное уравнение: 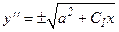(57)

Уравнение (57) относится к виду (45). Решим его.

;

;

;

;

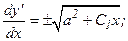
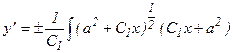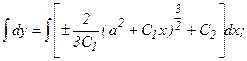
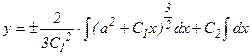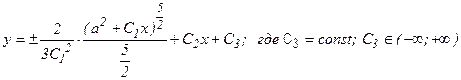. (58)

Итак, формула (58) определяет общее решение заданного уравнения (55).

Проверим, не потеряли ли мы решения, наложив ограничение z²– a² ≠ 0, т.е. z ≠ ± а.

Пусть z = ± а, т.е. у^|| = ± а. Откуда после двукратного интегрирования находим:

(59)

Непосредственной проверкой убеждаемся, что семейство функций (59) является решением заданного уравнения (55) (действительно, подставив (59) в (55) имеем тождество ), причем оно не может быть получено из общего решения (58) ни при каком наборе числовых значений произвольных С1, С2, С3.

Окончательно, совокупность всех решений уравнения (55) следующая

Ответ:

3. Уравнение вида: F (y, y^|, y^||,….y⁽ⁿ⁾)= 0 (60)

Отличительная особенность уравнения (60) в том, что оно явно не содержит независимую переменную х. Порядок такого дифференциального уравнения можно понизить на единицу, если положить у^/ = z (где z = z(у) – новая искомая функция, а у – новый аргумент). В этом случае производные у^//, у^///,…находятся (согласно правилу дифференцирования сложной функции) по формулам:

(61)

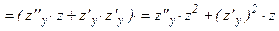и т. д.

Дата добавления: 2014-01-07