Пример. Являются ли функции линейно зависимыми на ?

Являются ли функции 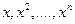линейно зависимыми на ?

Решение. Составим линейную комбинацию из данных функций: . По следствию из основной теоремы алгебры, у многочлена степени n с действительными коэффициентами может быть только n корней, поэтому тождественное равенство нулю для линейной комбинации для любого х из указанного промежутка возможно только при условии 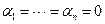. Следовательно, предложенная совокупность функций является линейно независимой.

Однако, решить вопрос о линейной зависимости или независимости функций на основании лишь данного выше определения возможно лишь в очень простых случаях. В общем случае этот вопрос решается следующей теоремой:

Теорема. Если непрерывные и (n-1) раз дифференцируемые на некотором интервале функции 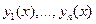- линейно зависимы, то на этом же интервале определитель Вронского (польский математик, 1775 – 1853 г.), составленный для этих функций, будет тождественно равен нулю:

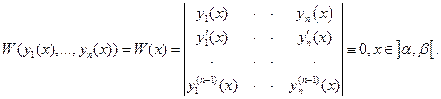(69)

Доказательство. Составим равную нулю линейную комбинацию из n линейно зависимых функций и продифференцируем её (n-1) раз:

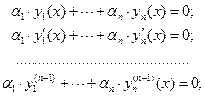(не все коэффициенты, входящие в линейную комбинацию, равны нулю).

Для любого фиксированного 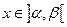написанная выше система уравнений относительно коэффициентов 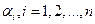является системой линейных однородных алгебраических уравнений, имеющей ненулевое решение. А это может быть лишь в случае, если определитель, составленный из коэффициентов при неизвестных (а это – определитель Вронского) равен нулю. Теорема доказана.

Замечание. Если данные функции – линейно независимы на промежутке 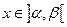, то составленный из них определитель Вронского может принимать нулевое значение лишь в конечном числе точек этого промежутка.

Отметим важное свойство решений ЛОДУ. Если функции 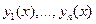- линейно независимы на промежутке 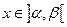, и каждая из них одновременно является решением ЛОДУ, удовлетворяющего условиям теоремы Коши на этом промежутке, то определитель Вронского для этих функций не обращается в нуль ни в одной точке этого промежутка: . (Свойство приводим без доказательства).

Теорема. Общим решением ЛОДУ порядка n, удовлетворяющего условиям теоремы Коши, является линейная комбинация из n его линейно независимых на 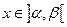частных решений 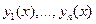, взятых с произвольными постоянными коэффициентами :

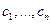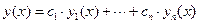. (70)

Доказательство. Утверждение, что линейная комбинация (70) – решение ЛОДУ, вытекает из свойства 1) ЛОДУ (см. выше). Решение (70) будет общим, если оно содержит в себе все частные решения. Зададимся произвольными начальными условиями: . Так как ЛОДУ удовлетворяет условиям теоремы Коши, то выбранным начальным условиям будет соответствовать единственное частное решение, которое может быть получено следующим образом. Для выбранных начальных условий можно записать:

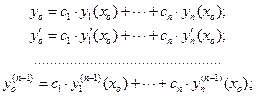(71)

Система уравнений (71) относительно произвольных констант – линейная алгебраическая неоднородная. Её определитель совпадает с определителем Вронского, который отличен от нуля в силу отмеченного ранее свойства решений ЛОДУ. Следовательно, ранг системы равен числу неизвестных и решение у системы (71) – единственное, т. е. набор констант = единственный для любого набора начальных условий задачи Коши.

Следствие. Максимальное число линейно независимых частных решений ЛОДУ порядка n, составляющих его общее решение, равно порядку уравнения, т. е. равно числу n. Легко показать, что если составить общее решение из (n+1)- ого частного решения то ранг системы, аналогичной системе (71), будет равен n и «лишний» (n+1) столбец войдёт в решение только для n констант .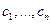

Любые n линейно независимые решения ЛОДУ порядка n составляют его фундаментальную систему решений.

Дата добавления: 2014-01-07