Линейные дифференциальные уравнения порядка n

Линейным дифференциальным уравнением порядка n называется уравнение, в котором неизвестная функция У и её производные до порядка n входят линейно.

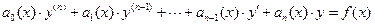(67)

Если правая часть 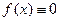, то уравнение называется однородным. Если в уравнении (67) коэффициент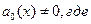 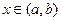, то оно приводится к каноническому виду путём деления всех его членов на этот коэффициент:

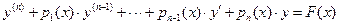(68)

Линейные однородные уравнения

Теорема существования и единственности решения Коши для ЛОДУ принимает следующую форму:

Если коэффициенты 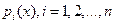- непрерывны на 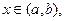то уравнение

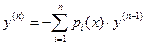удовлетворяет условиям теоремы Коши для уравнения, разрешенного относительно старшей производной. Поэтому для любой точки (n+1) -

мерного пространства 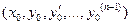существует и притом единственное решение ЛОДУ, определённое в некотором интервале, содержащем точку и удовлетворяющее начальным условиям: .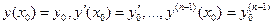

Отметим некоторые свойства ЛОДУ.

1). Если функции 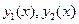- решения ЛОДУ, то линейная комбинация этих решений с любыми числовыми коэффициентами вида 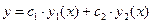так же будет решением этого уравнения. Свойство распространяется на любое конечное число решений уравнения.

2). Если ЛОДУ с коэффициентами – функциями действительного переменного 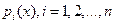имеет комплексное решение 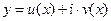, то действительная часть этого решения – функция и коэффициент при мнимой части – функция 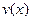каждая в отдельности так же являются решениями ЛОДУ. Доказательство свойства вытекает из общего свойства комплексных чисел: сумма, разность, произведение, частное комплексных чисел, сопряжённых с данными, есть комплексное число, сопряжённое с суммой, разностью, произведением, частным исходных комплексных чисел.

3). Всякое ЛОДУ имеет «нулевое» (тривиальное) решение.

Перед тем, как перейти к вопросам решения ЛОДУ, введём понятие линейной зависимости и независимости функций, аналогичное понятиям линейной зависимости и независимости системы векторов в линейном векторном пространстве.

Функции 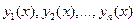назовём линейно зависимыми на сегменте ,если существуют постоянные коэффициенты 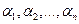такие, что для 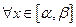выполняется тождественное равенство: 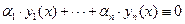, при этом не все постоянные коэффициенты 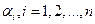равны нулю. Если указанное тождество выполняется лишь при условии 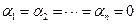, то функции называются линейно независимыми.

Дата добавления: 2014-01-07