Пример 10. Решение. Уравнение (62) есть уравнение 2-го порядка, не содержащее явно независимую переменную х, а поэтому оно относится к виду (60)

Решить задачу Коши: 2уу^// = (у^/)² + 1 (62)

у (0) = 1

у^/ (0) = -1 (63)

Решение. Уравнение (62) есть уравнение 2-го порядка, не содержащее явно независимую переменную х, а поэтому оно относится к виду (60). Понизим порядок данного уравнения (62) на единицу, положив у^/ = z (y). Откуда .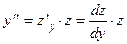

После подстановки у^/ = z и в уравнение (62) имеем:

(64) Уравнение (64) представляет собой уравнение 1-го порядка с разделяющимися переменными. Решим его. . Пологая, что у ≠ 0, делим обе части последнего уравнения на : ;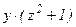

.

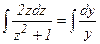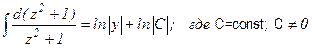
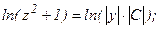
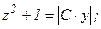
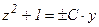Приняв С₁ = ± С (C₁ = const, C₁ ≠ 0), имеем:

.

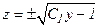Но, так как z = y^|, то после обратной подстановки получаем следующее дифференциальное уравнение: . Откуда 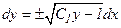. Пологая, что 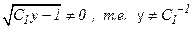, получаем: ;

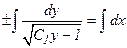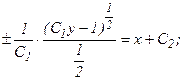
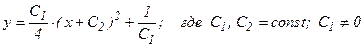. (65)

Итак, формулой (65) определяется общее решение заданного уравнения (62). Заметим, что в процессе решения налагались ограничения у ≠ 0 и у ≠ С^-1₁. Поэтому необходимо проверить, не утрачены ли при этом решения у =0 и у =С₁^-1. Функции у= =0 и у =С₁^-1, будучи подставленными в уравнение (62), не обращают его в тождество, а значит они не являются его решениями. Следовательно, формула (65) определяет все решения данного уравнения. Найдем частное решение уравнения (62), удовлетворяющее начальным условиям (63):

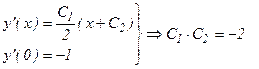
Получаем в результате систему: 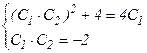, решением которой будет: С₁ = 2, С₂ = - 1. Таким образом, искомое частное решение имеет вид:

(66)

С геометрической точки зрения функция (66) определяет интегральную кривую (параболу с вершиной в точке и осью симметрии, параллельной оси ординат), проходящую на плоскости ХОУ через точку М_о (0; 1) и имеющую в ней касательную с угловым коэффициентом k = -1 (так как k = tgφ = -1, то касательная образует с положительным направлением оси Ох угол φ = 135⁰).

Дата добавления: 2014-01-07