Эллипс. Окружность

Линии второго порядка на плоскости.

Лекция 4.

Эллипс, окружность. Гипербола. Парабола.

Линии, уравнения которых в прямоугольной систем координат являются уравнениями второй степени, называются линиями второго порядка. К важнейшим линиям второго порядка относятся эллипс, окружность, гипербола и парабола.

Определение 4.1. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

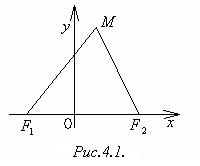Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние (рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.

Пусть M(x,y) ─ произвольная точка эллипса. Тогда по определению F₁M + F₂M = 2a > 2c, откуда a > c.

Так как F₁M = 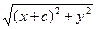, F₂M = 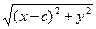, то имеем уравнение 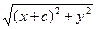+ 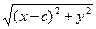= 2a.

Преобразуем это уравнение:

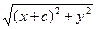()² = (2a − 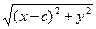)²,

(x² + 2cx + c²) + y² = 4a² – 4a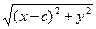+ (x² –­ 2cx + c²) + y²,

a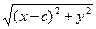= a² – cx.

Возводя в квадрат последнее уравнение, имеем

a²(x² – 2cx + c² + y²) = a⁴ – 2cxa² + c²x²,

(a² – c²)x² + a²y² = a²(a² – c²).

Так как a > c, то a² – c² > 0 и можем обозначить b² = a² – c². Тогда

b²x² + a²y² = a²b²,

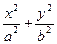= 1 (1)

Таким образом, координаты любой точки эллипса удовлетворяют уравнению (1).

Покажем обратное: если координаты точки M(x,y) удовлетворяют уравнению (1), то точка M лежит на эллипсе.

Из (1) найдём y²: y² = b²(1 - ).

Тогда F₁M = = = == = = ││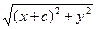

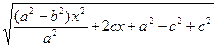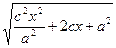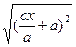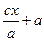Т.к. c < a и из (1) ≤ 1, т.е. x² ≤ a², │x│ ≤ a, то . Следовательно,

││= .

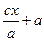Аналогично можно вычислить

F₂M = .

Теперь

F₁M + F₂M = .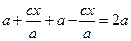

Из уравнения (1): b² > 0 Þ a² – c² > 0, т.е. a > c, откуда 2a > 2c. Значит, точка M лежит на эллипсе.

Уравнение (1) называется каноническим уравнением эллипса. Изображён эллипс с уравнением (1) на рис 4.2.

Точки пересечения эллипса с осями координат называются вершинами эллипса. Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осями называют также отрезки A₁A, B₁B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью, b ─ малой полуосью. Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси, т.е.

ε = .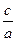

Так как 0 c < a, то 0 ε < 1. Фокальными радиусами точки M называют отрезки F₁M и F₂M. Их длины r₁ и r₂ вычисляют по формулам

r₁ = a + εx,

r₂ = a – εx.

Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a² = b² – c².

В случае, когда a = b, уравнение (1) принимает вид

= 1 или x² + y² = a²

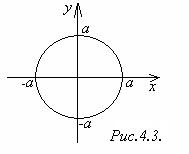
и определяет окружность радиуса а с центром в начале координат (рис.4.3). В этом случае c = 0, поэтому ε = 0.

Из школьного курса известно уравнение окружности радиуса R с центром в точке A₀(x₀,y₀):

(x – x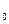)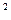+(y – y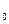)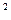=R.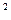

Такое уравнение называют каноническим уравнением окружности.

Дата добавления: 2014-01-07