Уравнение фигуры на плоскости

Тема 13. Геометрические образы на плоскости и в пространстве

Что такое джиттер?

Что такое время ожидании?

Что такое синхронизация?

Что такое сжатие файлов?

Какие факторы влияют на полосу пропускания и пропускную способность сети?

Факторы, влияющие на полосу пропускания и производительность:

• сжатие файлов и совместимость файловых форматов;

• синхронизация;

• время ожидания;

• джиттер

Сжатие файлов – это процесс, используемый для уменьшения размера обычного файла с помощью различных методов. Методы сжатия важны потому, что при уменьшении размера файла уменьшается время передачи файла в точку назначения, что влияет на производительность сети

При совместной передаче речи, видео и данных по сети вся эта информация должна быть синхронизирована программами у получателя, т. е. нужно, чтобы все последовательные фрагменты были собраны и воспроизведены в правильном порядке

Время, необходимое для передачи информации передающего устройства к принимающему, называется временем ожидания. Если полоса пропускания сети недостаточна, время ожидания увеличивается

Джиттер – разброс значений времени ожидания в сети, вызывающие заметные ошибки в доставке мультимедийного сигнала. Величина джиггера определяется путем вычитания минимального значения времени ожидания из максимального значения

Геометрической фигурой или просто фигурой на плоскости будем называть множество точек на плоскости. Задать фигуру — значит ука­зать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравне­ний с двумя неизвестными. Произвольное уравнение с двумя неизвест­ными x и y будем записывать в виде F(x, у) = 0.

Выберем на плоскости некоторую прямоугольную систему коорди­нат. В этой системе координат уравнение F(x, у) = 0 называется урав­нением фигуры 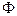при выполнении следующих двух условий:

1) если точка M(а,b) принадлежит фигуре 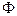, то координаты (а,b) точки М являются решением уравнения F(x, у) = 0, т. е. F(a, b) = 0 — верное числовое равенство;

2) если же пара чисел (с, d) является решением уравнения F(x,у) = 0, то точка N, координатами которой служат числа c и d, принадлежит фи­гуре .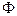

Из определения уравнения фигуры следует, что фигура 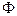состоит только из тех точек плоскости, координаты которых являются решени­ями уравнения F(x,у) = 0, т. е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1) дано уравнение F(x, у) = 0, и надо построить фигуру 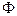, уравне­нием которой является F(x, у) = 0;

2) дана фигура 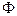, и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения F(x, у) = 0 и решается чаще всего методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1) задать фигуру геометрически, т. е. сформулировать условие, кото­рому удовлетворяют только точки фигуры (довольно часто определе­ние фигуры содержит такое условие);

2) записать в координатах условие, сформулированное в первом пункте.

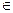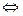
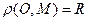Пример.1. Окружность Ф с центром в точке О и радиусом R задается условием M Ф, где 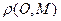— расстояние между точками O и М. Запишем это условие в координатах. Пусть центр O окружности имеет координаты (а,b), а через (x,у) обозначим координаты произ­вольной точки. Тогда условие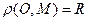в координатах имеет вид =.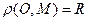

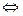
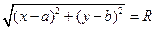
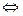
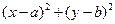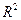Последнее уравнение, называется каноническим уравнением окружности с центром в точке O (а, b) и радиусом R.

Дата добавления: 2014-01-15