И перпендикулярности прямых

Угол между прямыми. Условие параллельности

Углом между прямыми и назовем не тупой угол 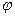, образующийся при пересечении и . Если || , то угол между и считаем равным нулю. Пусть прямые и заданы общими уравнениями соответственно прямые и заданы общими уравнениями соответственно

: , : .

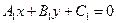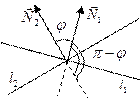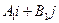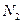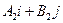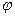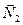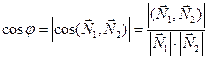Отложим нормальные векторы = , и = от точки пересечения прямых , и (рис. 2). Тогда угол между и равен одному из двух углов, которые могут образовать векторы и при всех возможных положениях их относи­тельно друг друга. Так как сумма этих углов равна , то , откуда получается формула

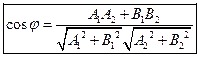(13.11)

Если прямые и заданы уравнениями с угловым коэффициентом соответственно

(13.12)

то угол между прямыми найдем по формуле

(13.13)

Для того чтобы прямые и были параллельными, необходимо и достаточно, чтобы: 1) их нормальные векторы и 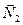были коллинеарными;

2) и были различны.

Отсюда ясно, что необходимым и достаточным условием параллельности прямых

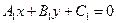: и : является ус­ловие

(13.14)

Если и заданы уравнениями с угловым коэффициентом, то условие параллельности имеет вид:

Для того чтобы прямые и были перпендикулярными, необходимо и достаточно, чтобы векторы и 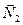были орто­гональными, т. е. = 0. Записывая скалярное произведе­ние в координатах, получим условие перпендикулярности пря­мых и :

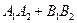=0. (13.15)
Если и заданы уравнениями с угловым коэффициентом, то прямые перпендикулярны тогда и только тогда, когда = 0 или .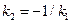

3) Если и совпадают, тогда

(13.9)

Если и заданы уравнениями с угловым коэффициентом, то условие параллельности имеет вид: . Если и совпадают, тогда .

Для того чтобы прямые и были перпендикулярными, необходимо и достаточно, чтобы векторы и 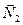были орто­гональными, т. е.

= 0. 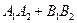= 0. (13.10)
Если и заданы уравнениями с угловым коэффициентом, то прямые перпендикулярны тогда и только тогда, когда = 0 или .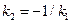

13.4. Расстояние от точки до прямой.

Введем на плоскости декартову систему координат Оху. На плоскости возьмем произ­вольную точку 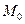(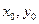) и прямую l, заданную общим уравнением

Ах + By + С = 0, (13.11)

Выведем формулу для расстояния точки 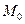от прямой l. Пусть 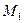() - основание перпендикуляра, опущенного из точки 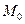на прямую l. Так как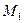 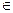l, то координаты точки 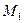удовлетворяют уравнению (13.11), т. е.

(13.12)

Рассмотрим скалярное произведение векторов 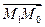и нормального вектора прямой l - =(А, B). Так как 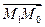||, то

откуда ==

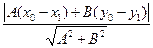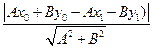
Из (13.12) следует,что 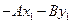= С, поэтому для расстоя­ния d (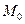, l) от точки 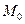до прямой l окончательно получим следующую формулу:

(13.13)

Пример 4. Найти расстояние от точки 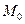(2,5) до прямой l, заданной уравне­нием

3x + 4у - 1 = 0. Имеем .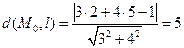

Дата добавления: 2014-01-15