Общее уравнение прямой на плоскости

	рис. 13.1

Пусть на плоскости введена декартова система координат Oxy и пусть l — некоторая прямая. Фиксируем на l какую-нибудь точку 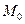с координатами 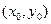и какой-нибудь ненулевой вектор N, перпендикулярный прямой l (рис.13.1). Ясно, что заданием точки 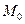и вектора N прямая l определяется однозначно. Пусть вектор N имеет координаты (A, В), т. е. N = A i + B j, где i, j —единичные векторы вдоль осей x и у. Очевидно, что точка М(x,y) принадлежит прямой l тогда и только тогда, когда , т. е. когда выполняется равенство 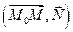= 0. За­писывая это равенство в координатах, получим уравнение прямой l, проходящей через точку и перпендикуляр­ной вектору N = A i + B j

А(х-х₀) + B(у-у₀)= 0.(13.2)

Это уравнение линейное. Таким обра­зом, доказана

Теорема 13.1. Всякая прямая на плоскости задается линейным уравнением.

Вектор, перпендикулярный прямой, называется нормальным вектором прямой. Уравнение (13.1) не зависит от выбора нор­мального вектора, поскольку все векторы, перпендикулярные l, коллинеарны и их координаты пропорциональны.

Теорема13.2. Всякое уравнение первой степени Ax + By + С = 0 задает на плоскости с декартовыми коорди­натами x, у некоторую прямую, перпендикулярную векто­ру N= Ai + Bj.

□ Так как хотя бы один из коэффициен­тов A, В отличен от нуля, то уравнение (13.1) имеет бесконечно много решений. Выберем произвольно одно из них — 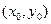. Тогда

Ах₀ + Ву₀ + С = 0. (13.3)

Вычитая почленно (13.3) из (13.1), получим уравнение

А(х-х₀) + B(у-у₀)= 0, (13.4)

равносильное уравнению (13.1). Как уже доказано, уравнение (13.2) задает прямую l, проходящую через точку , перпендикулярную вектору N = Ai + Bj. Так как уравнения (13.1) и (13.4) равносильны, т. е. имеют одно и то же множество решений, то уравнение (13.1) задает прямую l.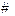

Уравнение (13.1) называется общим уравнением прямой.

Пример 2. Дана прямая 3x - у + 4 = 0. Написать уравнение прямой, прохо­дящей через точку 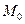(-1, 2) параллельно данной прямой.

Из теоремы 13.2 следует, что вектор v = (3, -1) перпен­дикулярен данной прямой. Так как данная и искомая прямые параллельны, то вектор v = (3, -1) перпендикулярен искомой прямой. Тогда прямая, параллельная данной, имеет уравнение 3(х+1)-(у-2) = 0 или 3х – у + 5 = 0.

Пример 3. Даны вершины треугольника A (1, -1), В (-2, 1), С (2, 4). Написать уравнение высоты AD, опущенной из вершины A на сторону ВС.

Решение. Высота AD перпендикулярна вектору ВС = (4, 3) и проходит через A (1, -1), и согласно теореме 13.1 ее уравнение име­ет вид 4(x - 1) + 3(у + 1) = 0 или 4х + 3у - 1 = 0.

Уравнение прямой с угловым коэффициентом.

Об­щим уравнением задается прямая при любом ее расположении относительно осей координат. Рассмотрим теперь прямые, не параллельные оси Oу. Для таких прямых удобно пользоваться так называемым уравнением с угловым коэффициентом.

Пусть l — прямая, не параллельная оси Oу, заданная общим уравнением

Ах + By + С = 0 (13.5)

Так как l D Oу, то В ­ 0, и, следовательно, уравнение (13.5) можно переписать в виде

Ax + By + C = 0 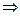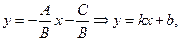(13.6)

где 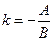- угловой коэффициент прямой l, 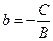- свободный член.

Коэффициенты в этом уравнении имеют «наглядный смысл». Ясно, что коэффициент b есть ордината точки пересечения прямой l с осью Oу. Выясним геометрический смысл k.

Пусть l пересекает ось Ox в некоторой точке P. Эта точка разбивает прямую l на два луча, один из которых Г лежит в полуплоскости у > 0. Углом между прямой l и осью Ox назовем угол между лучом Г и положительным направлением оси Ox. Тогда угловой коэффициент равен тангенсу угла k = tg . Если l параллельна оси Ox или совпадает с ней, то естественно считать, что = 0.

Еще раз отметим, что уравнение (13.6) вводится лишь для прямых, не параллельных оси Oy (иначе k = 4).

Век­торное уравнение прямой.

Пусть дана какая-нибудь точка 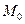и вектор 0, который считаем приложенным к точке :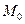

=

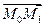
Эти данные определяют прямую l как геометрическое место концов всевозможных векторов вида

= t 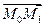, (13.7)

где t пробегает все вещественные числовые значения. Вектор =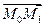, очевидно, является направляющим вектором прямой. Можно сказать, что наша прямая есть геометрическое место всех точек М, удовлетворяющих уравнению (13.7), а само это уравнение можно назвать уравнением прямой в векторной форме (или век­торным уравнением прямой). Ясно, что каждая прямая может быть задана, таким образом, какой-нибудь своей точкой 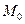и на­правляющим вектором = 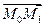. Существенным преимуществом уравнения (13.7) является то, что оно позволяет задать прямую не только на плоскости, но и в пространстве.

Дата добавления: 2014-01-15